Chapters
Welcome to our article on wave speed calculations and the factors influencing wave propagation. Waves surround us, from ripples in the water to the sound we hear. This article explores the wave speed formula's applications in various wave scenarios. You'll gain insights into wave mechanics by examining frequency, wavelength, and medium properties. We'll also provide step-by-step instructions for applying the formula.
Wave Speed
The concept of wave speed plays a crucial role in GCSE physics, offering valuable insights into the movement of waves and the transfer of energy within a medium. By measuring wave speed, we can determine the rate at which a wave travels and how quickly power is transmitted through a substance. This understanding helps us analyze wave propagation dynamics and its implications in different physical phenomena.
We can define wave speed as:
The rate at which a wave travels through a medium
OR
The distance traveled by a wave per unit of time
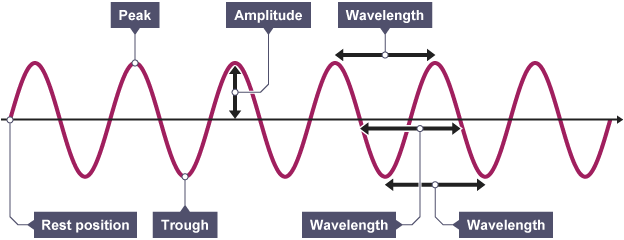
Calculating Wave Speed
The speed at which a wave travels can be determined using a simple equation that relates it to the wave's frequency and wavelength. Here's how it works:
The wave speed (v) is equal to the frequency of the wave (f) multiplied by its wavelength (λ):
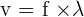
- The wave speed (v) is measured in meters per second (m/s)
- The frequency (f) is measured in hertz (Hz)
- The wavelength
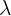is measured in meters (m)
Using this equation, we can understand how changing the frequency or wavelength affects the speed at which a wave travels through a medium. It helps us analyze and predict wave behaviour in different situations, providing insights into the fundamental nature of waves.
Factors Affecting Wave Speed
Main Factors
The primary factors that affect wave speed are frequency and wavelength.
- The frequency of a wave (number of wave cycles per second) and
- Its wavelength (distance between two corresponding points on a wave) is related to the wave speed.
As the frequency or wavelength increases, the wave speed also changes accordingly.
Other Factors
Other factors that may affect the speed of the wave are:
- Medium: The type of material through which the wave travels influences its rate.
- Tension or stiffness: For mechanical waves like waves on a string or in a spring, the stress or stiffness of the medium affects the wave speed: higher tension or greater stiffness results in higher wave speeds.
- Temperature: In gases and liquids, temperature plays a role in determining the speed of sound waves. As temperature increases, the speed of sound generally increases due to the increased kinetic energy of the particles.
Examples
1) A sound wave in the air has a frequency of 500 Hz and a wavelength of 0.7 meters. Calculate:
a) The wave speed of the sound wave
b) The period of the sound wave
Solution
Given information:
Frequency (f) = 500 Hz
Wavelength (λ) = 0.7 meters
a) To calculate the wave speed of the sound wave:
We can use the wave speed equation:
v = f * λ
Substituting the given values of frequency and wavelength:
v = 500 * 0.7
v = 350 meters per second (m/s)
Therefore, the wave speed of the sound wave is 350 m/s.
b) To determine the period of the sound wave:
We know that the time period (T) is the reciprocal of the frequency so we can use the formula:
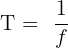
Substituting the given value of the frequency:
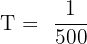
T = 0.002 seconds (s)
Therefore, the time period of the sound wave is 0.002 seconds.
Hence, the wave speed of the sound wave is 350 m/s, and The time period is 0.002 seconds.
2) A water wave has a wavelength of 1.5 meters and a wave speed of 2.5 m/s. Calculate:
a) The frequency of the water wave.
b) The time period of the water wave.
Solution
Given information:
Wavelength (λ) = 1.5 meters
Wave speed (v) = 2.5 m/s
a) To calculate the frequency of the water wave:
We can rearrange the wave speed equation to solve for frequency:
v = f * λ
Rearranging the equation:
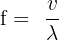
Substituting the given values:
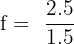
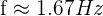
Therefore, the frequency of the water wave is approximately 1.67 Hz.
b) To determine the time period of the water wave:
The time period (T) is the reciprocal of the frequency so we can use the formula:
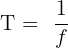
Substituting the value of the frequency:
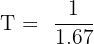
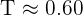seconds
Therefore, the time period of the water wave is approximately 0.60 seconds.
Hence, the frequency of the water wave is approximately 1.67 Hz, and The period of the water wave is about 0.60 seconds.
3) A radio wave has a frequency of 100 MHz and a wavelength of 3 meters. Calculate:
a) The wave speed of the radio wave.
b) The time period of the radio wave.
Solution
Given information:
Frequency (f) = 100 MHz (100 million hertz)
Wavelength (λ) = 3 meters
a) To calculate the wave speed of the radio wave:
We can use the wave speed equation:
v = f * λ
Substituting the given values of frequency and wavelength:
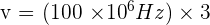meters
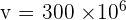meters per second (m/s)
Therefore, the wave speed of the radio wave is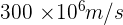 
.
b) To determine the period of the radio wave:
The time period (T) is the reciprocal of the frequency so we can use the formula:
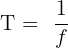
Substituting the given value of the frequency:
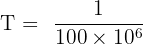Hz
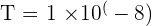s
Therefore, the time period of the radio wave is 1 × 10^(-8) seconds.
Hence, the wave speed of the radio wave is 300 × 10^6 m/s, and the period of the radio wave is 1 × 10^(-8) seconds.
Experiment 1
Experimenting with measuring the speed of sound directly between two points:
Setup:
- Select two individuals positioned approximately 100 meters apart.
- Use a trundle wheel to estimate the precise distance between them.
- Provide one person with two wooden blocks, which they will strike together above their head.
- Equip the second person with a stopwatch.
Procedure:
- The person with the wooden blocks initiates the experiment by striking them together.
- Simultaneously, the second person starts the stopwatch.
- The stopwatch is stopped when the sound of the blocks reaching the second person's location is heard.
- Repeat the process multiple times to ensure accuracy and calculate an average value for the time taken.
Calculation:
Using the average time measured, the speed of sound can be determined by employing the following equation:
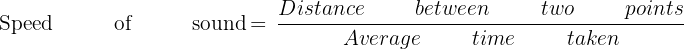
This experiment provides a practical means of directly measuring the speed of sound in air, allowing for hands-on exploration of acoustic phenomena and reinforcing critical principles of sound propagation.
Experiment 2
Measuring the speed of sound using echoes
Experiment setup:
- Position a person approximately 50 meters away from a wall or cliff, measuring the distance accurately with a trundle wheel.
- Equip the person with two wooden blocks and instruct them to clap them together.
- The person will listen attentively to the echo produced by the clap.
Experiment procedure:
- The person initiates the experiment by clapping the wooden blocks together.
- As soon as the person hears the echo, they begin clapping the blocks together repeatedly, in sync with the rhythm of the echoes.
- Simultaneously, a second person armed with a stopwatch starts timing when they hear one of the claps and stops timing after 20 claps have occurred.
- Repeat the process multiple times to ensure accuracy and calculate an average time from the recorded values.
Calculation:
Using the average time measured and the known distance between the person and the wall, the speed of sound can be calculated using the following equation:
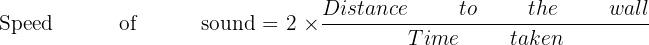
The total distance travelled by sound during the 20 claps equals two times the distance between the person and the wall, multiplied by 20 (20 × 2 × 50 meters).
Experiment 3
Measuring the speed of sound using an oscilloscope
Experiment setup:
- Connect two microphones to an oscilloscope.
- Position the microphones approximately 5 meters apart, accurately measured using a tape measure.
- Configure the oscilloscope to trigger when the first microphone detects a sound, and adjust the time base to visualize the sound arrival at both microphones on the screen.
- Have two wooden blocks ready to create a distinct clap near the first microphone.
Experiment procedure:
- Begin the experiment by producing a sharp clap using the wooden blocks next to the first microphone.
- Observe the oscilloscope display to determine the time the clap reaches each microphone.
- Note the time difference between the arrivals at the two microphones.
- Repeat the process to ensure accuracy and calculate an average time difference from the recorded values.
Calculation:
Using the average time difference measured and the known distance between the microphones, the speed of sound can be calculated using the following equation:
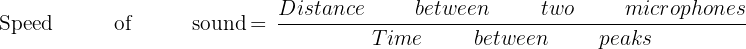
This experiment harnesses the capabilities of an oscilloscope to accurately measure the time difference between sound arrivals at different locations. It offers a unique and visual approach to determining the speed of sound while incorporating technology and encouraging an exploration of sound waves.
Experiment 4
Measuring the speed of ripples on water surfaces
Experiment setup:
- Select a calm, flat water surface like a lake or swimming pool.
- Position two individuals a few meters apart, accurately measuring the distance between them using a tape measure.
- Ensure one person is ready to disturb the water's surface while the other holds a stopwatch.
Experiment procedure:
- Begin the experiment with both individuals being prepared.
- The person who will disturb the water's surface starts a countdown from three.
- After the countdown, the person disturbs the water by creating a ripple using their hand or another method.
- As soon as the wave is made, the second person starts the stopwatch to time how long it takes to reach them.
- Repeat the process ten times, timing each instance, and record the values.
- Calculate the average time by adding the recorded times and dividing by 10.
Calculation:
Using the average time measured and the known distance between the individuals, the wave speed can be calculated using the following equation:
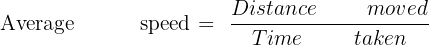
By applying the average time and distance, you can determine the speed at which the ripple travels across the calm water surface.
This experiment offers a practical and engaging way to measure wave speed using a natural setting and simple materials. It encourages observation, timing, and calculation skills, providing a hands-on approach to understanding wave motion on a water surface.
Did you like this article? Rate it!
Loading...
You are the best,, coz you have gotten content about the topics
Hello ! Glad to hear that you’ve found the content useful!