Chapters
Embark on a fascinating journey into wave interference, where waves combine and create unique patterns. We'll explore two types of interference: constructive and destructive, and understand how waves combine to produce these patterns. By learning about the conditions that lead to every kind of interference, we'll better understand this captivating phenomenon. Get ready to discover the secrets of wave interference in a way that is easy to grasp and appreciate.
Wave Interference
"Wave interference is the interaction between waves when they meet"
Imagine two pebbles dropped simultaneously into a tranquil pond. As the ripples from each stone expand outward, they eventually cross paths and merge. This blending of waves is interference. There are two types of interference: constructive interference and destructive interference.
Constructive interference
When two waves coincide with their peaks and troughs matching up, we say they are in phase. Imagine two waves with similar frequencies coming together in phase. When this happens, something interesting occurs called constructive interference.
Constructive interference means that the waves add up their energy to create a lock with a bigger amplitude. Think of it like two friends pushing a swing at the same time. The swing goes higher when they make it together than when they move individually. In the same way, when two waves combine in phase, their peaks and troughs line up perfectly, making the resulting wave stronger. It's like the waves join forces to become bigger and more powerful. Hence, we can say that:
In phase = Constructive interference
Constructive interference is an essential concept in physics, and we can see it in many everyday situations. For example, it explains why sound from multiple speakers can be louder when they're in phase and why specific colours appear brighter when different light waves combine.
So, remember, constructive interference is when waves come together in phase and combine their energy to make a more significant wave. It's like teamwork that makes the waves stronger and more impactful.
Destructive Interference
When two waves coincide, and the peaks of one wave align with the troughs of the other, we say they are out of phase. Imagine two waves with similar frequencies, like ripples on a pond, approaching each other. If their peaks and troughs align in opposite phases, they are said to be in destructive interference. Hence, we can say that:
Out of phase = Destructive interference
When waves experience destructive interference, their peaks and troughs coincide to cancel each other out. This leads to a reduced amplitude or even a complete elimination of the resulting wave. In other words, we can say that the two waves that are precisely out of phase will interfere destructively to generate zero amplitude. It's like two people pushing a swing at the opposite time, causing it to slow down or stop altogether.
Destructive interference can have interesting consequences. For example, when sound waves from speakers are out of phase, they can interfere and produce areas with reduced or no sound, known as "quiet spots" or "sound nulls." Similarly, in light waves, destructive interference can create dark regions in patterns, like when light passes through narrow slits and forms bands of light and dark on a screen.
Understanding destructive interference helps us make sense of various phenomena and enables us to analyze wave behaviour more deeply. So remember, when two waves meet, and their peaks and troughs align in opposite phases, they can cancel each other out, resulting in a weaker or nonexistent wave. It's like a dance move gone wrong, where the performers lose their impact.
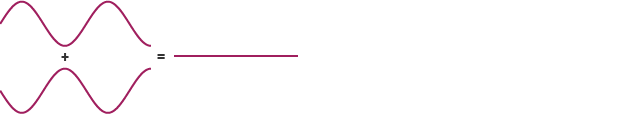
When Does Interference Happen?
Interference occurs when there is only one source of waves, and those waves travel different distances before they meet. For constructive interference to occur, the difference in the lengths travelled (called the path difference) must be a whole number of wavelengths. For destructive interference, the path difference must be an odd number of half wavelengths.
Everyday experiences only show constructive and destructive interference in waves. Examples include sound waves and water waves. We now understand that all electromagnetic waves also exhibit interference effects. 1801 Thomas Young conducted the first "double slit" experiment, demonstrating light interference. This experiment confirmed that light behaves like a wave, not a stream of particles.
Coherent Sources
Interference can also happen when there are two sources of waves, but there are some conditions:
- The sources need a consistent phase relationship, meaning they are in sync.
- The sources must have the same frequency so their phase relationship remains constant. These types of wave sources are called coherent sources.
Producing Interference Patterns Using Double Slit Experiments
When conducting a 'double-slit' experiment, it is possible to create an interference pattern for any wave. This occurs due to the phenomenon of diffraction, which causes the two slits to act as coherent sources.
Slits represent these coherent sources labelled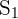 
and 
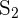. A wave detector can be systematically moved across the interference pattern to identify constructive and destructive interference points.
A screen displays the resulting interference pattern if visible light is used in the experiment. The screen is positioned parallel to the slits and visually represents the pattern formed at its surface.
Constructive Interference
The constructive interference occurs at the points at which a wave from reaches in phase with a wave from 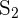. The path difference from 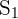and 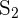should be the whole number of wavelengths.
Path difference =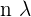 
, where n is an integer
Destructive Interference
Destructive interference happens at points where a wave from 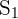and 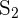reaches out of phase. For this, the path difference should be an odd number of half wavelengths:
Path difference =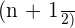 
, where n is an integer
Gratings
A grating contains several slits, or lines, that are close to each other. There is consistent spacing between the adjacent lines in a grind. Scrapes are also employed to create interference patterns. When waves are incident on the grating, all of the strings play the role of coherent sources of waves. Compared with a double slit, the interference pattern generated by the grating contains lesser, more widely spaced points with maximum intensity.
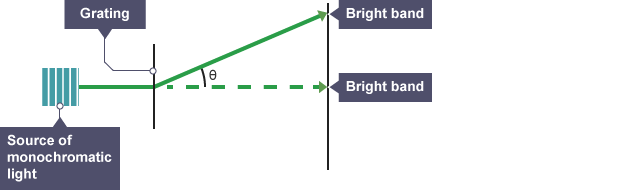
The above diagram shows how harshly it affects a monochromatic source of light. The central maximum is also known as zero order maximum. For other maxima orders, the relationship between the wavelength of light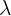 
and angle 
is demonstrated by the equation below:
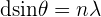
In the above equation:
- d stands for spacing of adjacent lines on the grating
- n represents the order number for the maximum
In the diagram, it would be:
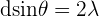
White Light and Spectra
The central maximum is white if white light is incident on the grating. Spectra are generated at the other order maxima. By considering the grating relationship:
- d is constant for any specific grating
- n is the same for each order maximum
Hence:
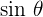only depends on a wavelength, which means that the bigger the wavelength, the bigger the angle.
Did you like this article? Rate it!
Loading...
You are the best,, coz you have gotten content about the topics
Hello ! Glad to hear that you’ve found the content useful!