Chapters
Waves are all around us, from the gentle ripples in a pond to the booming crash of ocean waves. Understanding their fundamental properties is critical to unravelling their mysteries. This article will delve into amplitude, wavelength, and frequency. We will explore their definitions, discover how they affect wave behaviour, and learn how to measure them. Get ready to ride the wave of knowledge!

What are Waves?
Waves are a fundamental concept in the study of energy and its transfer. They act as a means of transferring energy between different sources. They involve oscillations or vibrations around a central position. Hence, we can define waves as:
" The disturbances that carry energy through a medium or space without the transfer of matter"
They involve the movement or change of particles or fields.
Classification of Waves
Waves can be classified into two main types based on the direction of particle oscillation: longitudinal and transverse waves. Whether waves are longitudinal or transverse depends on the nature of oscillations.
- Longitudinal waves: They have vibrations parallel to the direction of wave propagation
- Transverse waves: They vibrations perpendicular to the direction of wave propagation.
Some more examples of waves are given below:
- Sound waves: They cause air particles to oscillate back and forth.
- Mechanical waves result in particle oscillations within solids, liquids, or gases and require a medium to travel through.
- Electromagnetic waves: They produce oscillations in electrical and magnetic fields.
It's important to note that all waves transfer energy but not matter. For instance, if a ball is placed on the surface of a pond and ripples pass by, the ball will move up and down but not be carried outward with the wave. Similarly, when sound waves travel through the air to reach a person's ear, the atmosphere remains stationary. Instead, the sound is conveyed through the vibrating molecules, which stay in place while oscillating around a fixed point.
Parts of Waves
Rest position
The rest position refers to the undisturbed part of particles or fields that do not vibrate. It is a reference point from which the wave's motion is measured. When a lock is present, particles or fields oscillate around this position.
Displacement
Displacement refers to the distance that a certain point in the medium has moved from its rest position. It represents the magnitude and direction of the wave's motion. Positive displacement indicates movement above the rest position, while negative displacement indicates movement below it.
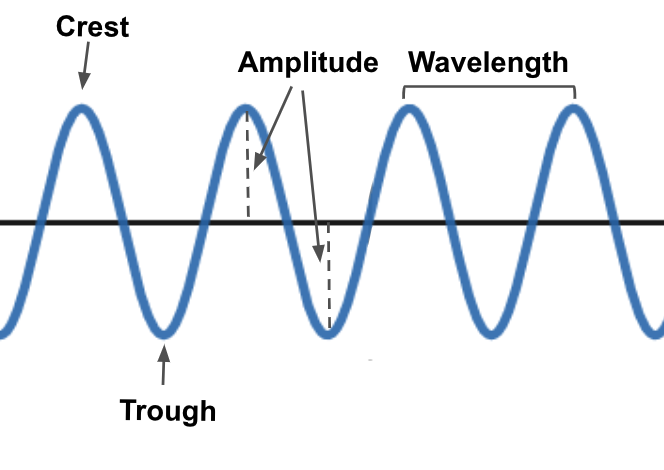
Peak
The peak of a wave is the highest point above the rest position. It represents the maximum positive displacement of the wave. It is often referred to as the wave's crest and corresponds to regions of maximum compression or upward displacement.
Trough
The trough of a wave is the lowest point below the rest position. It represents the maximum negative displacement of the wave. It is the opposite of the peak and corresponds to regions of maximum rarefaction or downward displacement.
Amplitude
Amplitude refers to the maximum displacement of a point on a wave from its rest position. It measures the intensity or strength of the wave. The greater the amplitude, the more energy the wave carries. Amplitude is usually measured from the rest position to the peak or the trough.
Wavelength
Wavelength is the distance covered by a complete cycle of the wave. It is commonly measured from peak to peak or trough to trough. Wavelength determines the spatial extent of the lock and is represented by the symbol λ (lambda). Waves with shorter wavelengths appear more closely packed, while waves with longer wavelengths appear more spread out.
Period
The period represents the time taken for a complete wave cycle. It is typically measured from peak to peak or trough to trough. The period is denoted by the symbol T and is inversely related to the wave frequency.
Frequency
Frequency is the number of waves passing a point each second. It measures how many complete cycles the wave undergoes in one second. Frequency is represented by the symbol f and is measured in hertz (Hz). The higher the frequency, the more waves pass by in a given time, indicating a higher pitch (for sound waves) or a higher energy (for electromagnetic waves).
Properties of Waves
The following three properties: amplitude, wavelength, and frequency, are interconnected and collectively determine the characteristics of a wave.
- Amplitude: A wave's amplitude refers to its maximum displacement or height from its equilibrium position. It is a measure of the wave's intensity or energy. In simpler terms, it represents the "height" of a wave.
- Wavelength: The wavelength of a wave is the distance between two consecutive points in a lock that is in the same phase, such as two crests or two troughs. It is usually denoted by the Greek letter lambda (λ) and is measured in meters. Wavelength determines the size or length of a wave.
- Frequency: The frequency of a wave is the number of complete cycles or oscillations it makes in one second. It is measured in hertz (Hz) and is denoted by the letter f. Frequency and wavelength are inversely proportional, meaning that as the frequency increases, the wavelength decreases, and vice versa.
How do Amplitude, Wavelength and Frequency Affect the Behavior of the Wave?
The properties: of amplitude, wavelength, and frequency impact how waves are perceived and interact with their surroundings.
- Amplitude: The amplitude of a wave determines its intensity or loudness (for sound waves) and brightness (for light waves). Larger amplitudes result in louder sounds and brighter light. Amplitude represents a wave's maximum displacement or height from its equilibrium position.
- Wavelength: The wavelength of a wave affects how it interacts with obstacles and boundaries. Waves with shorter wavelengths, such as high-frequency waves, are more easily diffracted, meaning they can bend around obstacles or spread out when passing through narrow openings. Waves with longer wavelengths, such as low-frequency waves, tend to travel in a more direct path and are less likely to diffract.
- Frequency: The frequency of a wave determines its pitch (for sound waves) and colour (for light waves). Higher frequencies correspond to higher-pitched sounds and colours towards the blue end of the visible spectrum. Lower frequencies correspond to lower-pitched sounds and colours towards the red end of the visible spectrum. Frequency also affects the energy of a wave, with higher frequencies carrying more fuel.
Calculating the period of a Wave
The period of a wave can be calculated using the formula:
Time period = 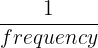
In this equation:
- The period (T) represents the time taken for one complete wave cycle and is measured in seconds (s).
- The frequency (f) is the number of complete cycles of the wave that occur in one second and is measured in hertz (Hz).
To calculate the period, divide one by the wave frequency.
Example
A water wave has a frequency of 2 Hz. Calculate the period of the wave.
Solution
Given: Frequency (f) = 2 Hz
We can use the formula:
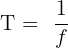
Substituting the given frequency into the formula:
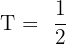
Using simple division, we can calculate the period:
T = 0.5 seconds
Therefore, the period of the water wave is 0.5 seconds.
This means it takes 0.5 seconds for the wave to complete one entire cycle, from peak to peak or trough to trough.
Calculating Wave Speed
To calculate the wave speed, you need to know the wavelength (λ) and the frequency (f) of the wave. The wave speed (v) can be determined using the following equation:
Wave Speed (v) = Wavelength (λ) × Frequency (f)
In this equation, the wave speed is measured in meters per second (m/s), the wavelength is measured in meters (m), and the frequency is measured in hertz (Hz).
Example
A wave has a wavelength of 2 meters and a frequency of 50 Hz. Calculate the wave speed.
Solution
Given:
Wavelength (λ) = 2 meters
Frequency (f) = 50 Hz
We can use the formula:
Wave Speed (v) = Wavelength (λ) × Frequency (f)
Substituting the given values into the formula:
v = 2 meters × 50 Hz
Multiplying the values:
v = 100 meters per second (m/s)
Therefore, the wave speed is 100 m/s.
This means that the wave is propagating through the medium at a speed of 100 meters per second. The wave speed represents how quickly the tide is moving and is determined by the product of the wavelength and frequency.












You are the best,, coz you have gotten content about the topics
Hello ! Glad to hear that you’ve found the content useful!