What Is The Quadratic Equation?
A quadratic equation is an equation of the form:
where a, b, and c are constants and a ≠ 0
The quadratic formula is used to find its solutions (or roots):
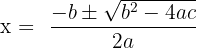
Quadratic equations often appear in real-world problems involving areas, motion, age, geometry, and product-sum relationships.
Quadratic Equation Practice Question and Answers
Determine the quadratic equation whose solutions are 3 and −2.
If x1 = 3 and x2 = −2,
then the equation is given by:
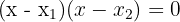
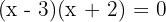
The quadratic equation is:
Find the value of k for which the roots of the equation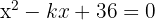 
are equal.
For equal roots, the discriminant must be zero:
Substitute a = 1, b = −k, c = 36:
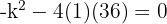
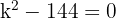
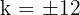
Values of k: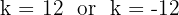 
The sum of two numbers is 5 and their product is −84. Find the numbers.
Let the numbers be x1 and x2.
We know: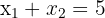
Equation: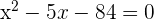 
Solve using factorisation: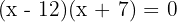
So,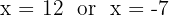 
The numbers are 12 and −7.
Within 11 years, Peter’s age will be half the square of the age he was 13 years ago. Find Peter’s current age.
Let Peter’s current age = x years.
Then:
Age 13 years ago = x − 13
Age in 11 years = x + 11
Equation: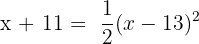
Multiply by 2 to clear the fraction: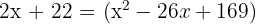
Simplify: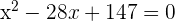
Factorise: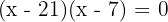
So,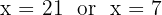 
Only x = 21 makes sense for an age.
Peter is 21 years old.
The perimeter of a rectangular field is 110 m, and its area is 750 m². Find its dimensions.
Let the length = x and breadth = y
Perimeter = 110 ⇒
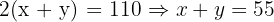
Area ⇒
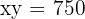
Substitute y = 55 − x: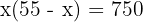
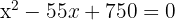
Solve: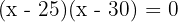 
So, x = 25 or x = 30
Dimensions: 25 m × 30 m
The sides of a right triangle are in the ratio 3 : 4 : 5, and its area is 24 m². Find the length of each side.
Let the sides be 3x, 4x, and 5x.
Area:
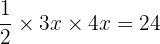
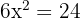
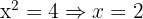
Sides: 6 m, 8 m, 10 m
Two natural numbers differ by 2, and the sum of their squares is 580. Find the numbers.
Let the numbers be x and x + 2.
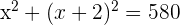
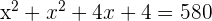
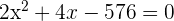
Divide by 2:
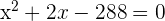
Factorise:
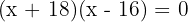
Numbers: 16 and 18
The diagonal of a rectangle is 75 m, and the sides are in the ratio 3 : 4. Find its dimensions.
Let the sides be 3x and 4x.
Using Pythagoras:
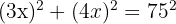
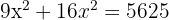
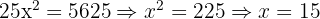
Sides: 45 m and 60 m
A rectangular garden 50 m long and 34 m wide is surrounded by a uniform path.
If the total area of the garden and path is 540 m², find the width of the path.
Let the width of the path be x.
Then the outer dimensions are 50 + 2x and 34 + 2x.
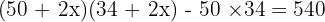
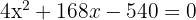
Divide by 4:
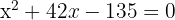
Solve:
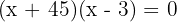
Width of path: 3 m
Two taps fill a swimming pool together in 2 hours.
Tap A alone takes 3 hours less than tap B. Find how long each tap takes individually.
Let tap A take x hours, tap B take x + 3 hours.
Work done in 1 hour:
A →
B →
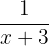
Together (as total time to fill is 2 hours) →
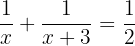
Multiply by:
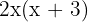
To give:
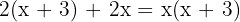
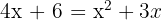
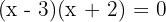
x = 3 (valid), x = −2 (discard)
Tap A = 3 hours, Tap B = 6 hours
Did you like this article? Rate it!
Loading...
I am impressed well done.