Chapters

Exercise 2
Solve:

Exercise 3
Solve:
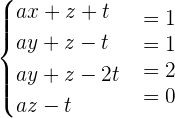
Exercise 4
Consider the following system for different values of a and b:
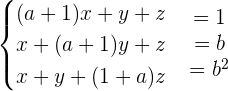
Exercise 5
Solve:

Exercise 6
Consider the following system for different values of a and b:
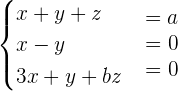
Exercise 7
Determine for what values of k, the following system has infinite solutions:

Exercise 8
Solve:

See what you should look out for in a Math tutor near me.
Solution of exercise 1
Solve:

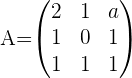

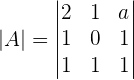
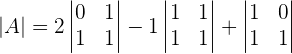

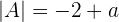
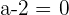
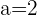

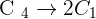

If a= , r(A) = r(A')=2, n=3
, r(A) = r(A')=2, n=3
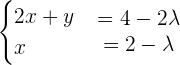

If  , this means that the system is a consistent independent system!
, this means that the system is a consistent independent system!
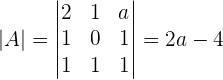
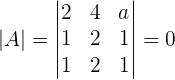
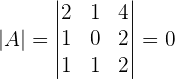
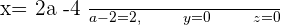
Solution of exercise 2
Solve:

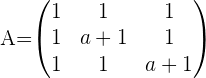
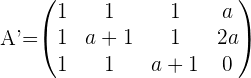
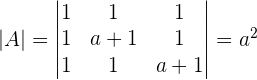
Supposing 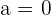 :
:
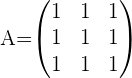

 , this means that the system is a consistent dependent system!
, this means that the system is a consistent dependent system!
 , supposing
, supposing 


In case,  , this means that the system is a consistent independent system!
, this means that the system is a consistent independent system!


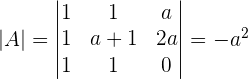
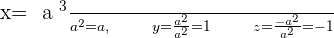
Solution of exercise 3
Solve:
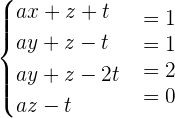

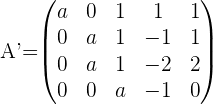
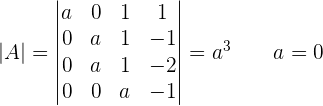
If 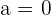



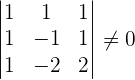
 , this means that the system is an inconsistent system!
, this means that the system is an inconsistent system!
If  this means that the system is a consistent independent system!
this means that the system is a consistent independent system!
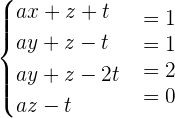
Applying row operation 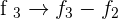 :
:
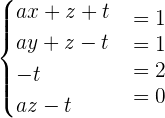

Solution of exercise 4
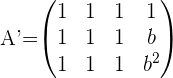
Consider the following system for different values of a and b:
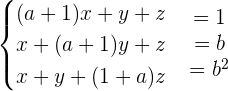
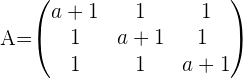


 , this means that the system is a consistent independent system!
, this means that the system is a consistent independent system!
If 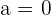 :
:


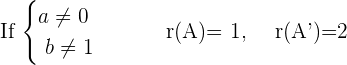 , this means that the system is an Inconsistent system!
, this means that the system is an Inconsistent system!
Otherwise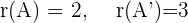 , this means that the system is a consistent dependent system!
, this means that the system is a consistent dependent system!
If  :
:




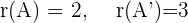 , this means that the system is an Inconsistent system!
, this means that the system is an Inconsistent system!
Solution of exercise 5
Solve:

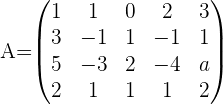
We will be using row operations:
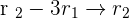
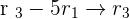


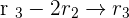

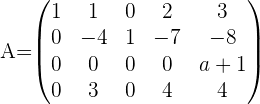
Finding the value of a from the 3rd row:
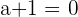
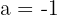
In the third row, 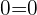 means that the system is a consistent dependent system.
means that the system is a consistent dependent system.
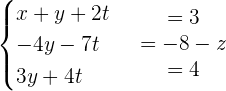

 which means inconsistent system.
which means inconsistent system.
Solution of exercise 6
Consider the following system for different values of a and b:
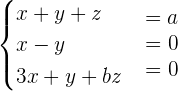
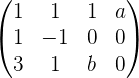
Applying these row operations:
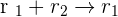

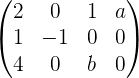
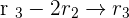
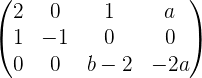
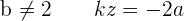 , hence it is a consistent indendent system
, hence it is a consistent indendent system

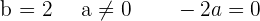 which indicates that the system is an inconsistent system
which indicates that the system is an inconsistent system
 which indicates that the system is a consistent dependent system
which indicates that the system is a consistent dependent system
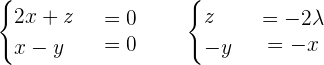

Solution of exercise 7
Determine for what values of k, the following system has infinite solutions:


Applying row operations:
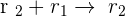
 * 2 was taken as common and divided by 0
* 2 was taken as common and divided by 0
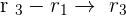
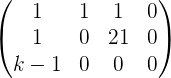
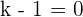
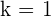
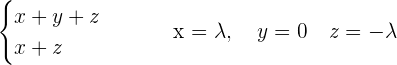
Solution of exercise 8
Solve:

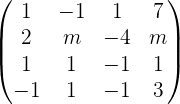
Applying these row operations:
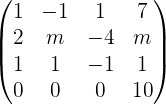
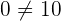 , this means that the system is an inconsistent system (for any value of m)
, this means that the system is an inconsistent system (for any value of m)
Learn more from Maths tutors near me on Superprof.
Get information about maths tuition here.
Summarise with AI:














I am impressed well done.