Chapters
In this article, we will discuss what is equality, what are equations, and their types. So, let us get started.

What is an Equality?
When two algebraic expressions are combined with an equal sign between them, we get equality.
Consider the following example:

You can see in the above equality two distinct algebraic expressions  and
and  are unified by an equal sign. Hence, we can say that it is equality.
are unified by an equal sign. Hence, we can say that it is equality.
There are two possibilities of an equality. It can either be true or it can be false. For instance, consider the following equality:



Hence, it is proved that the above equality is false.
Consider another equality below:

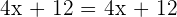
Hence, it is proved that the above equality is true.
Identity
An equality that is true for any value of the unknown variable is known as an identity
Consider the following example:



Hence, the above equality is true for any value of the variable x.
What is the Equation?
Unlike the identity, an equation is an equality that is true only for some values of the variables
For example, solve the equation below algebraically to find the value of unknown variable x.


The above equality is only true for x = 11, i.e. it has only one solution. Substituting any value other than 11 will not yield 6. Hence, the above equality is an equation.
The expressions on both sides of the equation are known as members of an equation. The terms of an equation are addends within the members of an equation. The members and terms of the equation are explained in the diagram below:

The variables or unknowns are the letters within the equation. For instance, in the above example, x is a variable. The solution of an equation is the value that makes an equation true. These solutions are also known as the roots of an equation. Consider the following example:


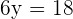

The value of y is 3 which is the root of the equation  because when it is substituted in the original equation, it makes the equation true.
because when it is substituted in the original equation, it makes the equation true.
Find various learn Maths online on Superprof.
Degree of an Equation
The degree of an equation is the degree of the largest term within it
Consider the following examples:

In the above polynomial, the highest degree of a term is 4. Hence, we can say that it is a fourth-degree polynomial.

The highest degree of a term is 3 in the above polynomial. Hence, we can say that it is a third-degree polynomial.

The highest degree of the term in the above polynomial is 2, hence it is a second-degree polynomial.
System of Equations
We have solved some examples above in which we computed the value of the unknown of a single equation. You can also be given two or more equations known as a system of equations. The system of equations are equivalent and have the same solution set.
Find the best maths tutor on Superprof.
Types of Equations
In mathematics, we have many different types of equations. These equations include linear equations, quadratic equations, cubic equations, exponential equations, differential equations, cubic equations, logarithmic equations, and so on. In this section, we will briefly discuss three types only.
Linear Equations
A linear equation is an equation of first degree. It means that the highest degree in linear equations is 1. By graphing linear equations in a coordinate plane, you will get a straight line. A linear equation can be written in the following three forms:
- Slope-intercept form: The slope-intercept form of the linear equation is
 . In this form, m is the slope and b is the y-intercept of the equation.
. In this form, m is the slope and b is the y-intercept of the equation. - General form: The general form of the linear equation is Ax + By + C = 0
- Point slope form: The point-slope form a linear equation is written as
 .
.
If an equation has a homogenous variable, i.e. it has a single variable only, then it is known as a linear equation in one variable. When a linear equation has two variables in it, then it is known as a linear equation in two variables. You can have two or more linear equations that have the same solution set. In some problems, you are given more than one such linear equations and you are asked to find their solution set. These equations are known as the system of linear equations and you can find their solution set by using either a substitution, elimination, or a graphing method.
Examples of Linear Equation
Quadratic Equations
The general form of the quadratic equation is  . The highest degree of a quadratic equation is 2. In other words, we can say that a quadratic equation is a second-degree polynomial. The values of x that satisfy a quadratic equation are known as zeroes or roots of the equation.
. The highest degree of a quadratic equation is 2. In other words, we can say that a quadratic equation is a second-degree polynomial. The values of x that satisfy a quadratic equation are known as zeroes or roots of the equation.
There are three methods to solve a quadratic equation. These methods are factoring, completing the square and quadratic formula. Sometimes by factoring a quadratic equation, you get a solution which when substituted in the original equation does not make the equation true. Such solutions are known as extraneous solutions. Completing the square method to find the roots of a quadratic equation is ideal when the roots of the equation are real or imaginary numbers.
We use a quadratic formula especially when the solutions to a quadratic equation are not rational numbers. The quadratic formula used to find the solutions of a quadratic equation is given below:
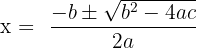
Examples
Some examples of the quadratic equations are given below:
You can see that some of the above equations are not equal to 0. You can always convert such equations into the general form of a quadratic equation by taking all the terms on the left hand side of the equation and putting zero on the right hand side.
Exponential Equations

Here, a is the base, y is the dependent variable and x is an independent variable or an exponent. The applications of exponential functions include population increase or decrease and radioactive decay.
You can check for a maths tutor here.
Summarise with AI:



















I am impressed well done.