Chapters

Introduction to Quadratic Formulas
In this article, we will explain the quadratic formula in detail. You will be familiar with the quadratic equation which is a second degree polynomial. It means that the highest degree of a quadratic equation is 2. The general form of the quadratic equation is given below:
 , where
, where 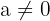
The solutions or the values of x of the quadratic equation are known as roots or zeroes of that equation. There are three methods to calculate the roots or zeros of the quadratic equation. These three methods are factoring, completing the square and quadratic formula. The method of factoring is straightforward. All you have to do is to find the factors the equation, set both the factors equal to 0, and solve for x. Completing the square method is often used when the roots of the equation are imaginary or real numbers. Most of the time the quadratic equation cannot be factored. In these cases, we employ a quadratic formula to compute the roots or zeroes of the equation. We especially use the quadratic formula when the roots of zeroes of the equation are not rational numbers. The quadratic formula to find the roots of the equation is given below:
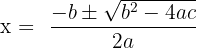
The part of the formula which is present under the radical sign  is known as a discriminant and it has the following three possibilities:
is known as a discriminant and it has the following three possibilities:
- If the discriminant
 is a positive number, i.e. it is greater than 0, then you will get two different roots
is a positive number, i.e. it is greater than 0, then you will get two different roots - If the discriminant
 is equal to zero, then you will get only one real solution to the quadratic equation
is equal to zero, then you will get only one real solution to the quadratic equation - If the discriminant
 is a negative number which means it is less than zero, then the quadratic equation has no real solution
is a negative number which means it is less than zero, then the quadratic equation has no real solution
In the next section of the article, we will solve a couple of examples in which we will find the roots of the quadratic equation using the quadratic formula.
Find the best maths tutor on Superprof.
Example 1
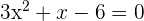
Solution
In this example, first, we will locate the values of a, b and c to substitute them in the quadratic formula.
Here, a = 3, b = 1 and c = -6.
Substitute these values in the formula below:
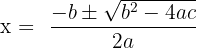
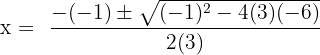
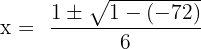
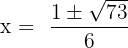
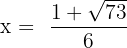 and
and 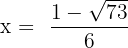
In decimal form, we will write them as:
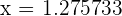 and
and 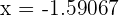
Example 2

Solution
In this example, first, we will write the equation in the form of a quadratic equation. A coefficient and a constant are on the right-hand side of the equation. We need to bring both the terms to the left-hand side and set the equation equal to 0.
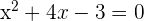
In the next step, we will locate the values of a, b and c to substitute them in the quadratic formula.
Here, a = 1, b = 4 and c = -3.
Substitute these values in the formula below:
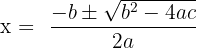
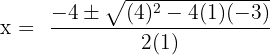
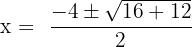
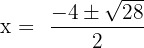
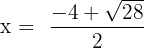 and
and 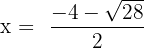
Simplifying the above answers will give us the roots in the decimal form:
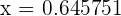 and
and 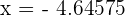
Example 3

Solution
In this example, first, we will write the equation in the form of a quadratic equation. A coefficient 3x and a constant 2 are on the right-hand side of the equation. We need to bring both the terms to the left-hand side and set the equation equal to 0.
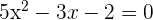
In the next step, we will locate the values of a, b and c to substitute them in the quadratic formula.
Here, a = 5, b = -3 and c = -2.
Substitute these values in the formula below:
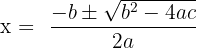
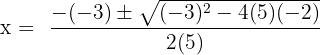
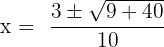
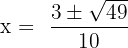
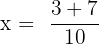 and
and 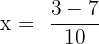
Simplifying the above answer will give us the following answers:
 and
and 
Find more learn Maths online here on Superprof.
Example 4
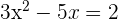
Solution
In this example, first, we will write the equation in the form of a quadratic equation. The constant 2 is on the right-hand side of the equation. We need to bring this term to the left-hand side and set the equation equal to 0.

In the next step, we will locate the values of a, b and c to substitute them in the quadratic formula.
Here, a = 3, b = -5 and c = -2.
Substitute these values in the formula below:
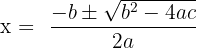
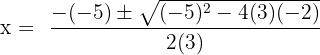
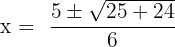
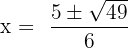
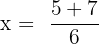 and
and 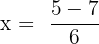
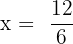 and
and 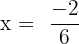
Simplifying the above answers will give us the following solutions:
 and
and 
Example 5

Solution
In this example, first, we will write the equation in the form of a quadratic equation. The constant 1 is on the right-hand side of the equation. We need to bring this term to the left-hand side and set the equation equal to 0.

In the next step, we will locate the values of a, b and c to substitute them in the quadratic formula.
Here, a = 8, b = - 2 and c = - 1.
Substitute these values in the formula below:
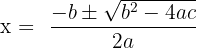
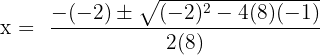
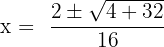
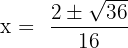
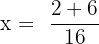 and
and 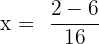
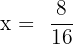 and
and 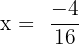
Simplifying the above answers will give us the following solutions:
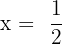 and
and 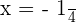
Example 6
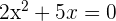
Solution
In this example, we are not given the value of c. When the value of c is not mentioned, then we can assume that it is equal to zero.
We already know that c = 0. Now, will locate the values of a and b substitute them in the quadratic formula.
Here, a = 2, b = 5 and c = 0.
Substitute these values in the formula below:
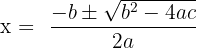
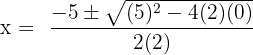
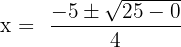
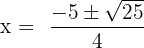
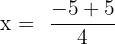 and
and 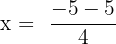
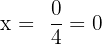 and
and 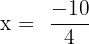
Hence, the roots of the equation are:
 and
and 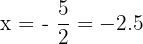
You can check for a maths tutor here.













I am impressed well done.