The word "Factoring" means to break down something big into its small portions. In the mathematical language, it means to break a number or equation into its factors. You can get the equation or number back by multiplying the factors with each other. Let's take an example of 24, the number "24" has a lot of factors such as if you multiply 6 and 4, you can get 24. The other factors are 8 and 3, 12, and 2, and not to forget that if you multiply 24 and 1, you will also get 24. The question is what is its usefulness?

Practical use of Factorization
Factorization helps us to find unknown variables. Imagine a linear equation, that linear equation is the rate of a chemical which is reacting per unit time. For an engineer, how he/she will know the amount of chemical needed for the reaction to proceed? To find that, the engineer needs to factorize the equation and equate it a number to find the value of the unknown. Furthermore, factorization is the standard way to show an equation. An equation like this 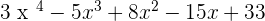 looks messy, however, a factorized equation looks much more engaging.
looks messy, however, a factorized equation looks much more engaging.
Factorization Methods
There are two methods of factorization and they are:
- Middle term breaking
- Quadratic Formula
The middle term breaking method is the easiest and shortest method to get factors of any equation. However, not all equations can be solved by the middle term method and that is why you can rely on the quadratic formula. You can find factors of any equation with the help of quadratic formula but using the quadratic formula is hard compared to the middle term breaking method. In addition, there is a big chance that you can make common mistakes when using the quadratic formula. That is why we recommend you use middle term breaking first but if the equation can't be factorized by the middle term breaking method then you should focus on the quadratic formula.
*Please do note that these methods are ONLY used for the quadratic equations(equations that has the power of x up to 2) only.*
Boost your learning speed and understanding with a maths tutor on Superprof.
Middle Term Breaking Method
Consider this equation: 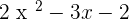
As the method says, you need to break the middle term into two factors. In the above equation, the middle term is  , you can get 3 with many factors but there are some conditions when selecting the right factors otherwise this method will fail. Let's address the above term into this form
, you can get 3 with many factors but there are some conditions when selecting the right factors otherwise this method will fail. Let's address the above term into this form  . So, the first step is to multiply a and c. In the above case, it will be
. So, the first step is to multiply a and c. In the above case, it will be  . Now you have the number which you need to break into factors. The next thing you need to check is the sign of the
. Now you have the number which you need to break into factors. The next thing you need to check is the sign of the  . If it is positive then the factors will be added and if negative then the factors will be subtracted. In the equation,
. If it is positive then the factors will be added and if negative then the factors will be subtracted. In the equation, 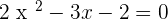 , the sign of
, the sign of  is negative, therefore, we will be subtracting factors of
is negative, therefore, we will be subtracting factors of  . Let's create factors of
. Let's create factors of  , here are the possible factors
, here are the possible factors  and
and  , and
, and  and
and  . If we subtract
. If we subtract  from
from  , we will get
, we will get  , however, if we subtract
, however, if we subtract  from
from  , we will get
, we will get  which is the value of
which is the value of  in the above equation. In conclusion, we will select factors
in the above equation. In conclusion, we will select factors  and
and  to factorize our equation.
to factorize our equation.

So, we broke  into
into 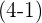 . Always double check your equation, if we subtract 1 from 4, we will get 3 which will result in the question equation. This means we are on the right path!
. Always double check your equation, if we subtract 1 from 4, we will get 3 which will result in the question equation. This means we are on the right path!
Multiplying the x with the factors:
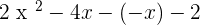

Taking common outside
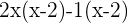
There is always something common, which is 1. Do you see that the variable and number in the brackets are the same? This means we are doing it correctly, it should be the same otherwise there is something wrong.
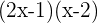
The above equations in brackets are the factors of  . Stop reading here and try to multiply the above two factors with each other and check what did you get. You see now what happened there?
. Stop reading here and try to multiply the above two factors with each other and check what did you get. You see now what happened there?
Examples:
1. 
Break the middle term:

Sign on the c = negative
Possible factors=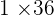 ,
,  ,
,  ,
,  ,
, 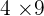
The middle term=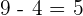 which means we will pick
which means we will pick 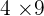 factor.
factor.
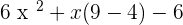

Taking common
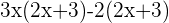
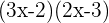
2. 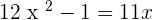
Re-arrange the equation:
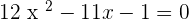
Break the middle term:
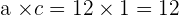
Sign on the c = negative
Possible factors= ,
, 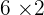 ,
, 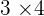
The middle term=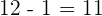 which means we will pick
which means we will pick 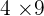 factor.
factor.
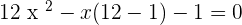
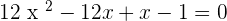
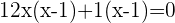
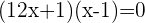


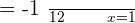
Quadratic Formula
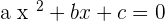
Dividing the whole equation by a:
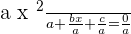


Making the left side a perfect square:
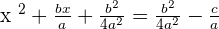

Taking root on both sides:
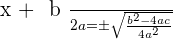

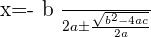
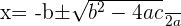
We will solve the above examples again but this time, we will use the quadratic formula. Remember, you can use quadratic formula for any quadratic equation.
Find various learn Maths online on Superprof.
Examples:
1. 
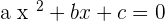
Comparing the both above equations:
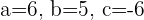
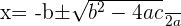
Substituting all the values of a,b, and c in the above equation:
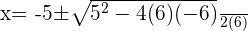
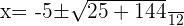
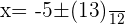
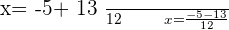


2. 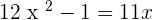
Re-arrange the equation:
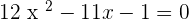
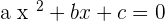
Comparing the both above equations:

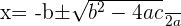
Substituting all the values of a,b, and c in the above equation:




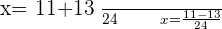
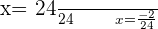
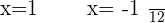
Find a maths tutor on Superprof today.
Summarise with AI:













I am impressed well done.