In this article, you will learn how to solve linear equations. But before proceeding to that, first, we will see what are the equations.

The best Maths tutors available

5 (69 reviews)

1st lesson free!

5 (48 reviews)

1st lesson free!

5 (32 reviews)

1st lesson free!

5 (62 reviews)

1st lesson free!

4.9 (163 reviews)

1st lesson free!

5 (69 reviews)

1st lesson free!

4.9 (27 reviews)

1st lesson free!

4.9 (50 reviews)

1st lesson free!

5 (69 reviews)

1st lesson free!

5 (48 reviews)

1st lesson free!

5 (32 reviews)

1st lesson free!

5 (62 reviews)

1st lesson free!

4.9 (163 reviews)

1st lesson free!

5 (69 reviews)

1st lesson free!

4.9 (27 reviews)

1st lesson free!

4.9 (50 reviews)

1st lesson free!
Let's go
Equations
An equation is an algebraic expression that contains an equality sign.
It depicts that the left-hand side of the equality is equal to the right-hand side. If you add or subtract the same thing on both sides of the equation, the equation will remain unaffected. There are different types of equations such as linear, exponential, quadratic and logarithmic, etc. In this article, our main focus will be the linear equations only.
An equation of a straight line is known as a linear equation.
For instance, the algebraic expression 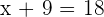 is a linear equation as it contains "=" sign. It means that x + 9 is equal to 18. So, what is the value of x?
is a linear equation as it contains "=" sign. It means that x + 9 is equal to 18. So, what is the value of x?
Well, the value of x will be such that both sides are equal. So, it must be 9 because 9 + 9 = 18. In this example, we have only one variable x. That is why it can be known as a linear equation in one variable. We can have an equation containing two or more variables. For instance, consider the following equation:
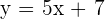
The above equation has two variables x and y. Hence, we can call it as a linear equation in two variables. It is also given in the slope-intercept form. A slope-intercept form of the linear equation is  . Here, m is the slope and b is a constant.
. Here, m is the slope and b is a constant.
Solving a linear equation in one variable is pretty straightforward. On the other hand, it is not possible to find the value of unknowns in the linear equation in two variables without knowing the value of one variable. To solve the linear equations in two variables, we often have two equations, so we can solve them as a system. Solving a system of linear equations is an entirely distinct concept, therefore in the next section, we will only focus on solving the linear equation in one variable.
Find more learn Maths online here on Superprof.
Steps for solving a linear equation in one variable
To solve a linear equation in one variable, follow these steps:
- First, remove the parentheses by solving the terms inside them.
- In the next step, simplify the terms with the denominators.
- Make two groups of the terms, one having the x variable and the other having the constants.
- Apply the arithmetic operations of addition or subtraction to similar terms to reduce them.
- Solve for unknown.
Find the best Maths tutor on Superprof.
Let us solve some examples in which we will follow the above steps to calculate the unknown. Example 1
Solve 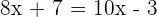 .
. Solution
The above equation does not have parentheses or a fraction, so we will simply solve it by isolating the variable on either side of the equation to find its value. First, subtract 8x from both sides of the equation. Remember that we are here utilizing the property of an equation which says that if the same thing is added or subtracted to both sides of the equation, then the equation remains unchanged. Now, we will add 3 to both sides of the equation: To find the value of x, we will divide both sides by 2: Example 2
Solve 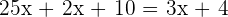 .
. Solution
There are no parentheses and fractions in the above equation too, hence we will isolate the variable x on either side of the equation to get the value of unknown. First, subtract 3x from both sides of the equation. Here, we are again using the property of an equation which says that if the same thing is added or subtracted to both sides of the equation, then the equation remains unchanged. Now, subtract 10 from both sides of the equation to isolate the term with the variable on the left-hand side: To find the value of x, we will divide both sides by 6: Example 3
Solve the equation 
Solution
This equation contains parentheses and fractions, hence we will solve it step by step like this: Step 1 - Remove parentheses
In the first step, we will remove the brackets like this: Step 2 - Remove the denominators
In this step, we will remove the denominators: Step 3 - Group similar terms together
In this step, we will group the terms with variable and without variable together: Step 4 - Add and subtract the similar terms
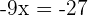
Step 5 - Solve for x
Divide both sides by -9 to get the value of x: Example 4
Solve the equation 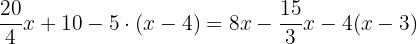
Solution
This equation contains parentheses and fractions, hence we will solve it step by step like this: Step 1 - Remove parentheses
In the first step, we will remove the brackets like this: Step 2 - Remove the denominators
In this step, we will remove the denominators to reduce the fractions: Step 3 - Group similar terms together
In this step, we will group the terms with variable and without variable together: Step 4 - Add and subtract the similar terms
Step 5 - Solve for x
Divide both sides by -1 to get the value of x: Example 5
Solve the equation 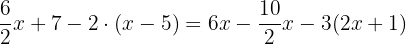
Solution
This equation contains parentheses and fractions, hence we will solve it step by step like this: Step 1 - Remove parentheses
In the first step, we will remove the brackets like this: Step 2 - Remove the denominators
In this step, we will remove the denominators to reduce the fractions: Step 3 - Group similar terms together
In this step, we will group the terms with variable and without variable together: Step 4 - Add and subtract the similar terms
Step 5 - Solve for x
Divide both sides by 6 to get the value of x: We will simplify the above answer by dividing the fraction by 2: Example 6
Solve the equation 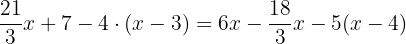
Solution
This equation contains parentheses and fractions, hence we will solve it step by step like this: Step 1 - Remove parentheses
In the first step, we will remove the brackets like this: Step 2 - Remove the denominators
In this step, we will remove the denominators to reduce the fractions: Step 3 - Group similar terms together
In this step, we will group the terms with variable and without variable together: Step 4 - Add and subtract the similar terms
Step 5 - Solve for x
Divide both sides by 8 to get the value of x:

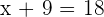 is a linear equation as it contains "=" sign. It means that x + 9 is equal to 18. So, what is the value of x?
is a linear equation as it contains "=" sign. It means that x + 9 is equal to 18. So, what is the value of x?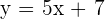
 . Here, m is the slope and b is a constant.
. Here, m is the slope and b is a constant.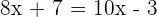 .
.
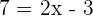
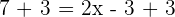


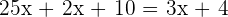 .
.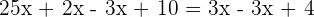


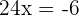
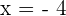

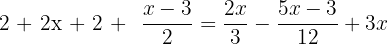
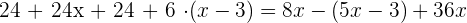
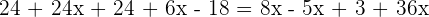

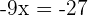

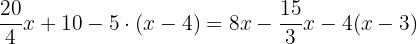
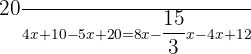
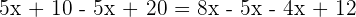
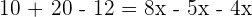

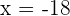
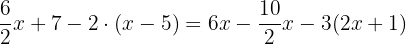
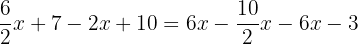
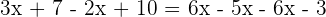

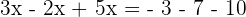
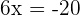
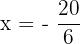
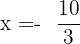
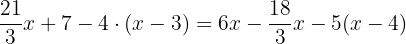
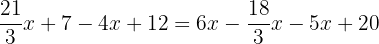
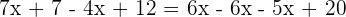
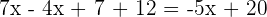


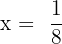













I am impressed well done.