Chapters
The word "equivalent" means equal in amount. Hence, equivalent equations mean that equations that have the same solutions. Finding solutions of equivalent equations isn't not only important in the world of Algebra, but we also use equivalent equations in our daily lives. Below is an example of equivalent equations.

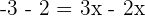
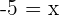

Now, if you substitute the value of x on both sides of the equation, you will get the same answer. In simple words, the left-hand side of the equation will be equal to the right-hand side of the equation. Hence, we draw a conclusion, whenever we deal with equivalent equations, the roots of both equations will be identical and if the roots are substituted, the right-hand side of the equation will always be equal to the right-hand side of the equation.
Boost your learning speed and understanding with a maths tutor on Superprof.

Criteria for Equivalence of Equations
There are some criteria that you need to follow if you are using any mathematical operations. Below are the criteria:
1. If two members of an equation are added or subtracted by the same amount, the equation is equivalent to that given.

Introducing  on both sides:
on both sides:
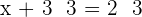
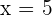
2. If two members of an equation are multiplied or divided by the same number (nonzero), the equation is equivalent to that given.
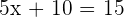
Dividing the both sides by  :
:

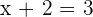
Subtracting 2 from both sides:


Equation with One Variable
If there is an equation with just one variable (with polynomial degree = 1) that means the equation is a linear equation. Linear equations are very simple to solve as well as understand. Imagine this equation:
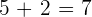
Now, let's replace the "2" with x which will be:

The above equation is a linear equation with just one variable. You know that you can use mathematical operations to solve for the unknowns. Below is how you will solve the linear equation with just one variable by applying mathematical operations on constants.

Introducing  on both sides:
on both sides:
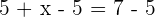

There are some rules to solve these types of equations, however, fundamental rules are already discussed but there are a few that are remaining to be discussed:
- You can raise the power of both sides of the equation and the power should be the same. The same goes for root as well.
- Raising both the power of both sides of the equation and they both are non-negative will result in the same even root and hence the equation will be an equivalent equation.
Equation with Two Variables
Things become more complicated when an equation has two unknown variables. In the above examples, we were considering only one variable and it is very simple to solve equivalent equations with just one variable. However, if there are two variables then you can't solve it easily. As a matter of fact, in order to find the solution of unknowns, you need another equation with the same variables and then solve them simultaneously to get the values of unknowns. Below is an example of equivalent equations with two unknown variables:
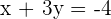 --- i
--- i
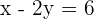 --- ii
--- ii
We have two unknown variables in both equations. You can only solve it simultaneously if the roots of both equations are the same. This means that the line of both equations intersects at a specific point.
Considering equation i and writing it in terms of x:
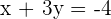
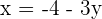 --- iii
--- iii
Substituting the value of x (which is the equation iii) in the equation ii:
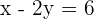
Since, 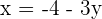 , therefore:
, therefore:


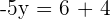

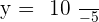

Hence, we found that the value of y is  but still we have one variable remaining and that is x. Now, we will substitute the value of y in either equation i or equation iii. We will be substituting the value in the equation iii:
but still we have one variable remaining and that is x. Now, we will substitute the value of y in either equation i or equation iii. We will be substituting the value in the equation iii:
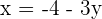
Since  , therefore:
, therefore:
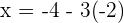
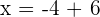

In conclusion, at  , the value of x for the both equivalent equations is
, the value of x for the both equivalent equations is  . Let's verify by substituting the value of x and y in both equations:
. Let's verify by substituting the value of x and y in both equations:
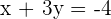 --- i
--- i
When  :
:
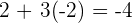

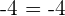
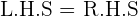
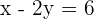 --- ii
--- ii
When  :
:
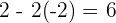


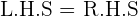
Find a maths tutor on Superprof today.
Summarise with AI:













I am impressed well done.