Chapters
Polynomial equations are very hard to solve. The most used method to find the factors of a polynomial equation is the trial and error method which will not only consume a lot of your time but it will also make anyone frustrated. Maths was discovered to make our lives easy not difficult and that is why we try to use the "Biquadratic Equations" method to solve polynomial equations.
Biquadratic Equations are a type of polynomial equation, however, this means that not all polynomial equations are biquadratic equations. The key is to check whether the polynomial equation has any odd-degree term? If you saw any odd degree term, that means the biquadratic method isn't applicable to that equation, unfortunately, you need to use trial and error method to solve that equation.
For example, here is an equation, check whether the equation has any odd-degree terms, 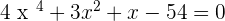 , take your time and think whether we can apply the biquadratic method on this equation? If your answer is no then congratulations! You learned when to use this method. The reason is pretty simple if you check the third term (that is
, take your time and think whether we can apply the biquadratic method on this equation? If your answer is no then congratulations! You learned when to use this method. The reason is pretty simple if you check the third term (that is  ), it is an odd-degree term. As mentioned above, you can't apply this method if the equation has an odd-degree term. Here is another example to test yourself,
), it is an odd-degree term. As mentioned above, you can't apply this method if the equation has an odd-degree term. Here is another example to test yourself,  , can we apply the biquadratic equation method to this equation? Yes, of course! Because there is no odd-degree term. The word odd doesn't mean that we are talking about odd numbers, don't get confused with odd numbers and odd terms. This is the last example, figure out whether we can use this method or not,
, can we apply the biquadratic equation method to this equation? Yes, of course! Because there is no odd-degree term. The word odd doesn't mean that we are talking about odd numbers, don't get confused with odd numbers and odd terms. This is the last example, figure out whether we can use this method or not,  , the answer is no because it is already in the form of the quadratic equation. We use the biquadratic equation method to convert polynomial equations into quadratic equations so that we can solve them easily by breaking the middle term method or by using the quadratic formula.
, the answer is no because it is already in the form of the quadratic equation. We use the biquadratic equation method to convert polynomial equations into quadratic equations so that we can solve them easily by breaking the middle term method or by using the quadratic formula.
Find a maths tutor on Superprof.

Solving Biquadratic Equations
Now you know the first thing about the biquadratic method and that is you can't apply to odd-degree term equations. The next thing that you need to understand is the conversion of the polynomial equation to the biquadratic equation. To do that, we use a technique that we call supposition. It is a very simple technique, you need to suppose a variable with a certain degree to another variable. For example, here is a polynomial equation:
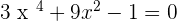
Here, we will suppose in such a way that the equation converts into a quadratic equation. The best part of supposition is that you can suppose anything, however, make sure it fits with your system. In simple words, you can suppose anything but in a limit so that you can work on your equation. For the above equation, we will suppose  . You can use any other variable than t, it can be a,b,c,d, etc. Let's substitute our supposition in the above equation:
. You can use any other variable than t, it can be a,b,c,d, etc. Let's substitute our supposition in the above equation:


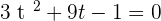
Now, that equation has been transformed into the quadratic equation that means our supposition was correct but this is not the end. You need to solve the above equation and get its factors, fortunately, we have already solved it, and here are the factors  . Why don't you take a small glimpse of the original equation? Did you notice something? The variable in the equation was
. Why don't you take a small glimpse of the original equation? Did you notice something? The variable in the equation was  , however, the variable in the answer is
, however, the variable in the answer is  . That happened because we substituted the variable
. That happened because we substituted the variable  , remember? Don't forget about this! This is a very common mistake. Students leave their answers in terms of
, remember? Don't forget about this! This is a very common mistake. Students leave their answers in terms of  which is not the answer. Once you find the factors of
which is not the answer. Once you find the factors of  , now it is time to put the original value back which was
, now it is time to put the original value back which was 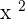 . You will do something like this:
. You will do something like this:

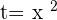

Taking roots on both sides:
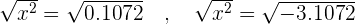
 *Because root of negative number means imaginary number.
*Because root of negative number means imaginary number.
Another common mistake is that students forget to add 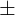 when taking roots of the factors. Remember, usually, biquadratic equations will have four answers but in a few cases, it can have two answers too.
when taking roots of the factors. Remember, usually, biquadratic equations will have four answers but in a few cases, it can have two answers too.
Find various learn Maths online on Superprof.
Examples
1 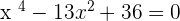
Let  :
:

You can use both methods (that are middle term breaking method and quadratic formula) to solve this equation, here we will be using the middle term breaking method to solve our equation:
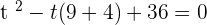
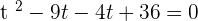
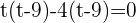
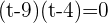


Substituting 



The same procedure can be used to solve the equations of the type:
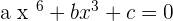


2 
Supposing 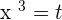
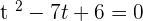
Using the quadratic formula to get factors:
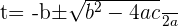

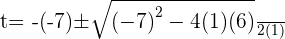
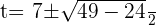
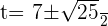

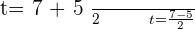
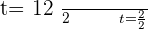

Substituting 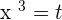


3 
Let  :
:
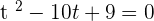
Using middle term breaking method to find factors:
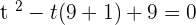
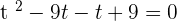
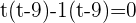
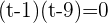


Substituting 

Taking root on both sides

4 
Let  :
:
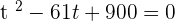
Using quadratic formula to find factors
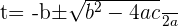


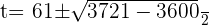

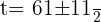
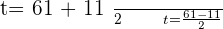
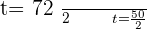

Substituting 
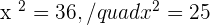
Taking roots on both sides

5 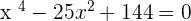
Let  :
:
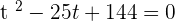
Using the middle term breaking method to find factors
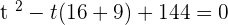
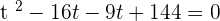




Substituting 


6 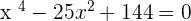
Let  :
:
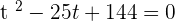
Using quadratic formula to find factors
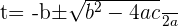

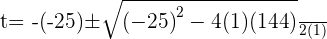
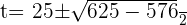





Substituting 


Boost your learning speed and understanding with a maths tutor on Superprof.













I am impressed well done.