Imagine a lot of linear lines that are meeting each other at different points. Solving these types of equations is practically impossible because analytical methods will consume a lot of time not to mention a small error can disturb the whole system. That is why we rely on numerical methods to solve different systems of linear equations.
Before we try to even solve the equation, we find its nature. This means that the system will either have a solution or not. Think about it, you tried to solve a system of equations and after a lot of hard work, you found that the specific system doesn't have a solution, that must be frustrating right? To avoid that, you can already find that either the system will have solutions or not through the ranking method.
To find the nature of the system, you should know how to find the rank of a matrix. The necessary and sufficient condition for a system of m equations and n unknowns has a solution where the range of the coefficient matrix and the augmented matrix are equal. Here are some rules that you should know:
- If the rank of the matrix is equal to the rank of the augmented matrix that means you are dealing with a consistent system. (Condition: R=R')
-
- If the rank of the matrix as well as the number of unknowns are equal that means it is a consistent independent system. (Condition: R=R'=n)
- If the rank of the matrix and the number of unknowns are NOT equal that means it is a consistent independent system. (Condition: R=R'≠n)
-
- If the rank of the matrix is NOT equal to the rank of the augmented matrix that indicates that the system you are working on is an Inconsistent system. (Condition: R≠R')
See what you should look out for in a Math tutor near me.

Steps to Solve a System of Equations
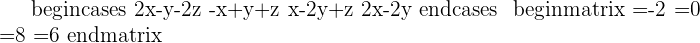
1. Find the rank of the matrix of coefficients:
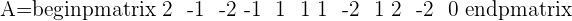
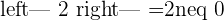
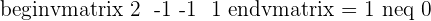
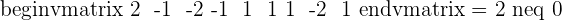

2. Find the rank of the augmented matrix:
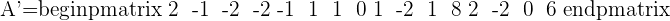


3. Study the obtained information and determine which type of system it is:
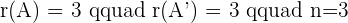
Since this fulfill this condition "Condition: R=R'=n", hence we can say that this system is consistent independent system.
4. Solve the system if it is not inconsistent, by Cramer's rule or the Gauss elimination method.
Take the system corresponding to the submatrix of order 3, which has a rank of 3, and solve it:





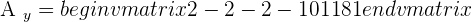
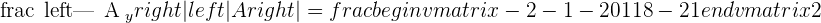
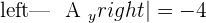
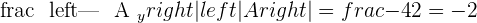
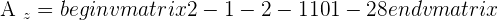

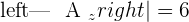

Example 1

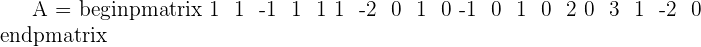


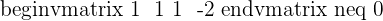

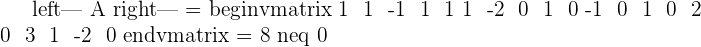
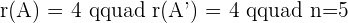
Since this fulfill this condition "Condition: R=R'≠n", hence we can say that this system is consistent dependent system.
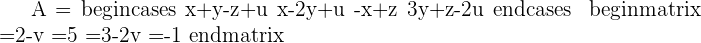
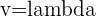
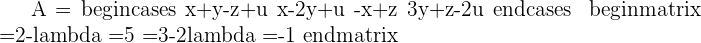
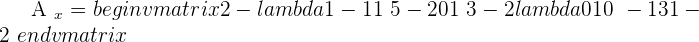
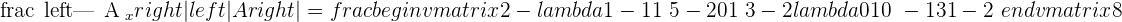
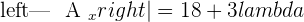

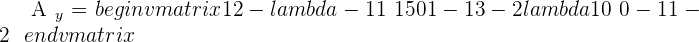

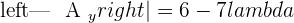

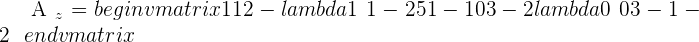

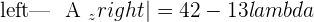


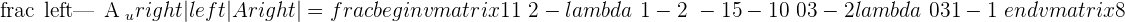
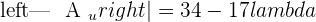

Example 2
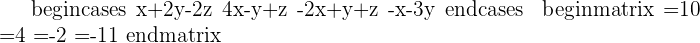
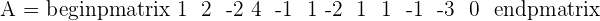
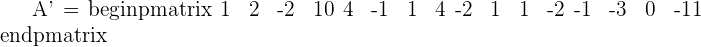


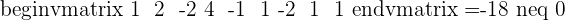

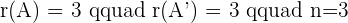
Since this fulfill this condition "Condition: R=R'=n", hence we can say that this system is consistent independent system.
Example 3.
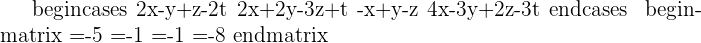
Study and resolve the system, if possible:
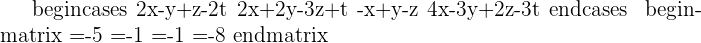

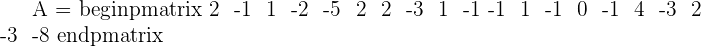
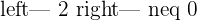
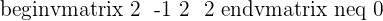
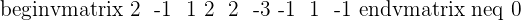


Since this fulfill this condition "Condition: R=R'=n", hence we can say that this system is consistent independent system.
Learn more from Maths tutors near me on Superprof.
Get information about maths tuition here.













I am impressed well done.