Chapters
In the world of linear algebra, Cramer's rule plays a very important role in finding determinants, ranks, and type of system. In simple words, Cramer's rule is used to find the solution of a system of a linear equation. In addition, it also helps us to identify whether the system will have at least one solution or not. This saves a lot of time and not to mention that this method is very accurate to predict solutions of a system.
There is another method to find a solution to a linear system which is known as the Gauss Elimination method. At this point, you might be wondering why should we use Cramer's rule instead of the Gauss Elimination method? We have an answer. Cramer's rule is very simple to use. You have to follow a similar pattern for all of the matrix, on the other hand, Gauss Elimination requires logical row operations. You need to think and select the row operations. These row operations can become difficult when solving a system of a linear equations system. Furthermore, there are operations when considering Gauss elimination such as row pivoting and column operations. They have their own rules which can become frustrating sometimes.
Check for a maths tutor here.

How does Cramer's Rule work?
To make things easy, imagine a system which has two linear equations:
 (1)
(1)
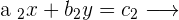 (2)
(2)
We can eliminate one variable with the help of row operations. You can choose any variable but here, we chose to eliminate y to make equation in term of x. To do that, we need to apply a row operation. If we multiply equation 2 by the 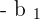 and equation 1 by the
and equation 1 by the  and then add both equations, we can easily eliminate y from the overall equation.
and then add both equations, we can easily eliminate y from the overall equation.
 hence
hence 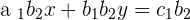
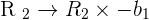 hence
hence 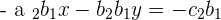
Adding both equations:
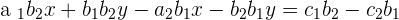
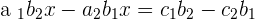
Taking x as a common:

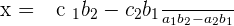

Now, the same method will be applied but this time, we will eliminate x and make the equation in terms of y.
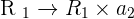 hence
hence 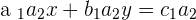
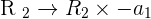 hence
hence 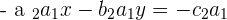
Adding both equations:
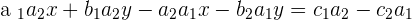

Taking y as common:

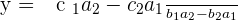

Did you notice something? The denominator of both equations are same. That denominator is the determinant of the coefficient matrix. Therefore, we can write something like this:


Where,  is the determinant of the coefficient matrix,
is the determinant of the coefficient matrix,
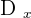 is the determinant of the numerator in the x solution,
is the determinant of the numerator in the x solution,
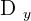 is the determinant of the numerator in the y solution.
is the determinant of the numerator in the y solution.
In the above example, we considered a system of two equation but what if you don't have system of two equations? Then still, you don't need to worry because the method is exactly the same. Here is an illustration if you have number of system:

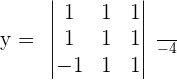
Determinants are obtained by replacing the coefficients of the 2nd member (independent terms) in the 1st, 2nd, 3rd and the nth column, respectively. However, there are some conditions to use Cramer's rule, below are all the conditions.
- The number of equations equals the number of unknowns.
- The determinant of the coefficient matrix is nonzero.
Examples
Example 1
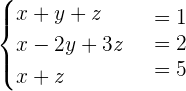
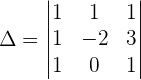

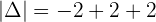
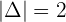

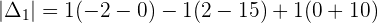
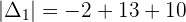
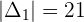
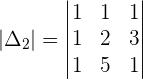
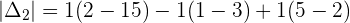
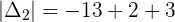
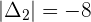
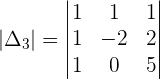
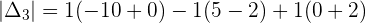

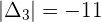


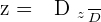
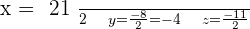
Example 2
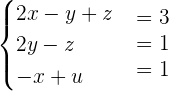
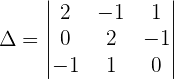





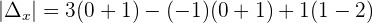
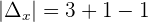
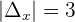



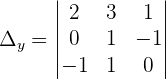
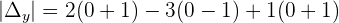
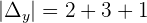
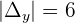
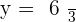

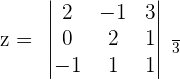

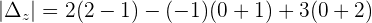
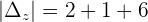
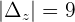

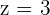
Example 3
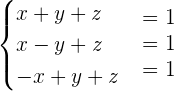

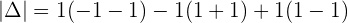
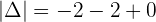
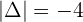
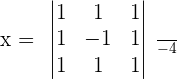
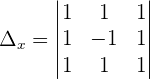
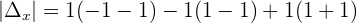



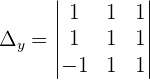
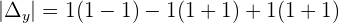
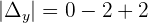

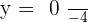

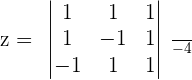

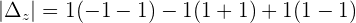
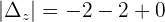
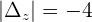
Find a maths tutor on Superprof.
Summarise with AI:













I am impressed well done.