In this article, you will learn what are radical equations and how to solve them. You are already familiar with equations. The equations have an equality sign between them and the left and right-hand sides of the equations are equal. Do you know what are radical equations?
Well, before discussing the radical equation, you must know what the radicals are. Just like the addition and subtraction are opposite to each other and multiplication is an inverse of the division operation, the radical is opposite to the exponent. A radical expression is an expression that has a constant, coefficient or variable under the root 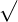 symbol. For instance,
symbol. For instance, 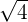 ,
,  and
and 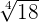 are radicals because they involve the radical sign. Now, let use define radical equations:
are radicals because they involve the radical sign. Now, let use define radical equations:
An equation in which the variable is under the root or radical sign is known as a radical equation
Radical equations are also known as irrational equations. In other words, we can say that the unknown values in the radical equations are present under the radical sign. In the next section, we will learn what are the steps involved in solving a radical equation.
You can check for a maths tutor here.

Steps to solve a radical equation
You should follow the following steps to solve a radical equation:
- First, you should isolate the radical expression from the equation which involves a variable. If there are two or more radical expressions involving a variable, then isolate one of them.
- According to the index of the radical expression raise both sides of the equation to the index or power. For instance, if the radical expression involves a square root function, then take the square of both sides of the equation.
- Repeat steps 1 and 2, in case there is a radical expression left. If there is no radical expression left, then solve the equation for the unknown value.
- Substitute the value of the unknown in the original equation to see if the equation is true for that value or not.
In the next section, we will solve a couple of examples which will make the whole concept of solving radical equation more clear.
Find the best Maths tutor on Superprof.
Example 1
Solve the following equation:

Solution
Follow these steps to solve the equation:
Step 1 - Isolate the radical
First, we need to isolate the radical by taking any variable or constant to the other side of the equation. In this example, we will take x to the right-hand side of the equation:

Step 2 - Take square of both sides of the equation
Since we have a square root function in this example, hence in this step, we will take square of both sides of the equation:

Step 3 - Solve the equation for the unknown value
Now, we have the equation, we can easily solve it to find the value of x:
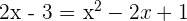

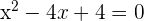
You can either use quadratic formula to get the value of x or factorize the above equation like this:
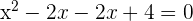
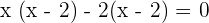
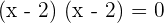

Step 4 - Substitute the value in the original equation
To check whether your solution is true or not, we should substitute the value of x in the original equation to see if the equation is true for that value or not:

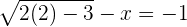
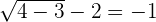
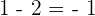
Example 2
Solve the following equation:
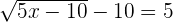
Solution
Follow these steps to solve the equation:
Step 1 - Isolate the radical
First, we need to isolate the radical by taking any variable or constant to the other side of the equation. In this example, we will take -10 to the right-hand side of the equation:
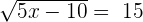
Step 2 - Take square of both sides of the equation
Since we have a square root function in this example, hence in this step, we will take square of both sides of the equation:
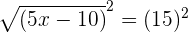
Step 3 - Solve the equation for the unknown value
Now, we have the equation, we can easily solve it to find the value of x:

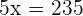

Step 4 - Substitute the value in the original equation
To check whether your solution is true or not, we should substitute the value of x in the original equation to see if the equation is true for that value or not:
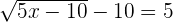
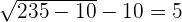
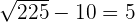
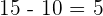
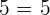
Example 3
Solve the following equation:

Solution
Follow these steps to solve the equation:
Step 1 - Isolate the radical
First, we need to isolate the radical by taking any variable or constant to the other side of the equation. In this example, we will take -3 to the right-hand side of the equation:
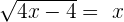
Step 2 - Take square of both sides of the equation
Since we have a square root function in this example, hence in this step, we will take square of both sides of the equation:
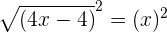
Step 3 - Solve the equation for the unknown value
Now, we have the equation, we can easily solve it to find the value of x:
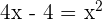
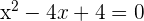
You can either use quadratic formula to get the value of x or factorize the above equation like this:
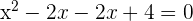
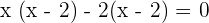
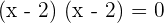

Step 4 - Substitute the value in the original equation
To check whether your solution is true or not, we should substitute the value of x in the original equation to see if the equation is true for that value or not:


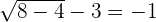

We know that the square root of 4 is 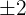 . In this case, we can take 2 to make the equation true:
. In this case, we can take 2 to make the equation true:
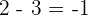
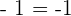
Example 4
Solve the following equation:

Solution
Follow these steps to solve the equation:
Step 1 - Isolate the radical
First, we need to isolate the radical by taking any variable or constant to the other side of the equation. In this example, we will take - x + 3 to the right-hand side of the equation:
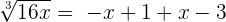
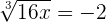
Step 2 - Take a cube of both sides of the equation
Since we have a cube root function in this example, hence in this step, we will take a cube of both sides of the equation:

Step 3 - Solve the equation for the unknown value
Now, we have the equation, we can easily solve it to find the value of x:
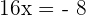
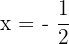
Step 4 - Substitute the value in the original equation
To check whether your solution is true or not, we should substitute the value of x in the original equation to see if the equation is true for that value or not:

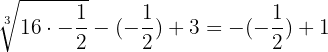
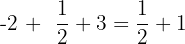
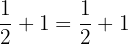
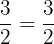
Example 5
Solve the following equation:
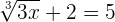
Solution
Follow these steps to solve the equation:
Step 1 - Isolate the radical
First, we need to isolate the radical by taking any variable or constant to the other side of the equation. In this example, we will take + 2 to the right-hand side of the equation:
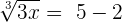

Step 2 - Take cube of both sides of the equation
Since we have a cube root function in this example, hence in this step, we will take cube of both sides of the equation:
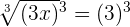
Step 3 - Solve the equation for the unknown value
Now, we have the equation, we can easily solve it to find the value of x:

Divide both sides by 3:
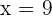
Step 4 - Substitute the value in the original equation
To check whether your solution is true or not, we should substitute the value of x in the original equation to see if the equation is true for that value or not:
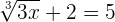
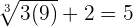
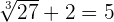
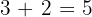
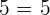
Find more learn Maths online here on Superprof.













I am impressed well done.