Chapters
Solving multiple linear lines by using analytical methods will consume a lot of time. Not to forget that a single error can cost you a lot. That is why we prefer numerical methods to predict the solution. When it comes to solving, there are two methods that you can rely on, one is solving a linear system by Cramer's rule and the second is the Gauss Elimination method.

Solving a Linear System of Equations with Parameters by Cramer's Rule
In this method, we will use Cramer's rule to find rank as well as predict the value of the unknown variables in the system. Below is an example of a linear system that has one unknown variable.
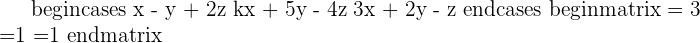
Here, k is the unknown variable. The first step is to convert the system into the coefficient matrix and augmented matrix.
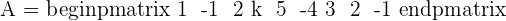
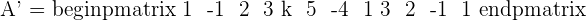
A represents the coefficient matrix and A' represents the augmented matrix. The next step is to find the determinants of both matrices.
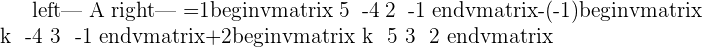
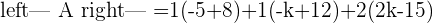
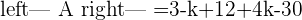
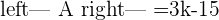
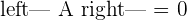
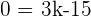
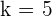
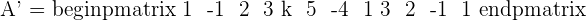
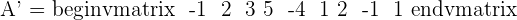
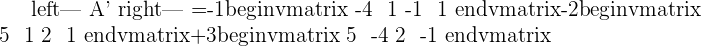
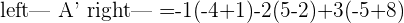
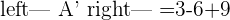
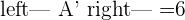
Once you found both matrices determinant, the next step is to find the rank of both matrices.
If 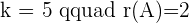
If 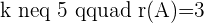

With the help of the ranks, now you can determine the type of system.
If 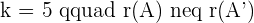 , hence the system will be Inconsistent system.
, hence the system will be Inconsistent system.
If 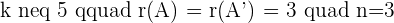 , hence the system will be Consistent independent system.
, hence the system will be Consistent independent system.
Since we know what type of system we are dealing with, now we can focus on finding the solution of the linear system. This equation can also be solved by the Gauss Elimination method but right now we are focusing on Cramer's rule.
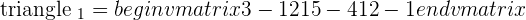
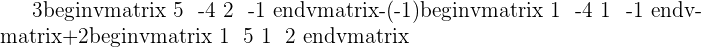
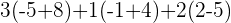
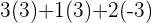
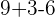
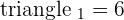
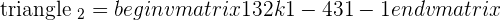
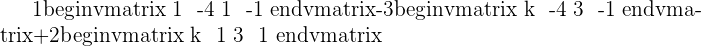
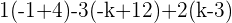
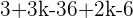
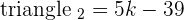
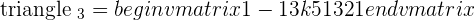
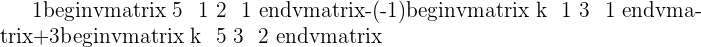
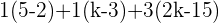
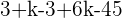
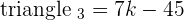
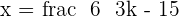
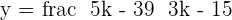
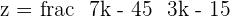
Check for outstanding maths tutors near me here.
2. Solving a Linear System of Equations with Parameters by the Gauss Elimination Method
Gauss Elimination is a direct method in the numerical analysis which helps to find determinant as well as the rank of a matrix. Basically, direct methods provide a precise answer but on a condition that they are performed in infinite precision. Gauss Elimination suggests that through row operations, we can find the determinant and the rank of the matrix. Sometimes, you might need to do some partial pivoting but it is not necessary.
In Gauss elimination, we need to convert the augmented matrix into an upper triangular matrix. In case, if you don't know the upper triangular matrix then it is a matrix where all the elements below the diagonal are zero. Here is an illustration of the upper triangular matrix.
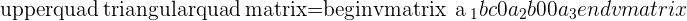
In this upper triangular matrix, 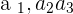 are the diagonal elements and rest variables are constants. If you multiply all the diagonals elements then you will get the determinant of the matrix. It needs to be determined whether there is any value of m to make the system consistent. If so, solve the system for that value of m.
are the diagonal elements and rest variables are constants. If you multiply all the diagonals elements then you will get the determinant of the matrix. It needs to be determined whether there is any value of m to make the system consistent. If so, solve the system for that value of m.
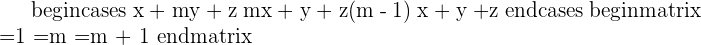
Convert it to augmented matrix:
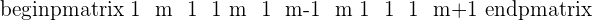
Row operations: 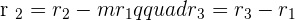
If you look at the left side of the row operation, that means you are applying row operation to that specific row. The right side of row operation shows the operation that you want to apply on that specific row. Do note that these row operation will be applied to the whole row.
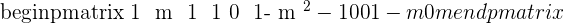
In addition, you can shift column too. For example, in the above matrix, if we swap column 2 and 3, we can easily get an upper triangular matrix.
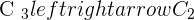
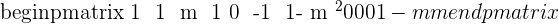
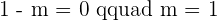
If 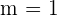 , this means
, this means 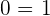 , hence the system will be Inconsistent system.
, hence the system will be Inconsistent system.
If 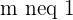 , this means that the system will be a Consistent dependent system.
, this means that the system will be a Consistent dependent system.
Examples
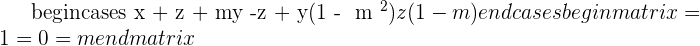
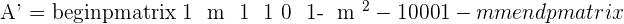
Since the matrix is already in the form of upper triangular matrix, we can use backward substitution directly to find values of x, y, and z.
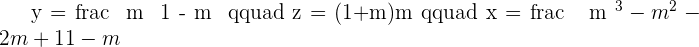
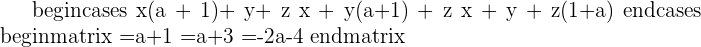
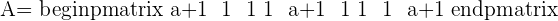
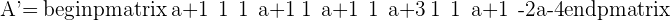
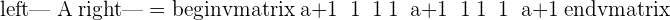
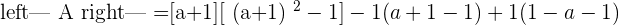
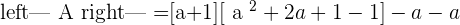
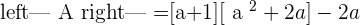
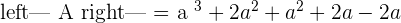
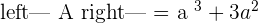
Hence, there will be two solutions, either 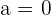 or
or 
If 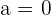
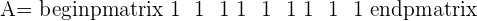
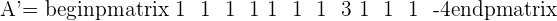
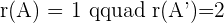 hence the system will be Inconsistent system
hence the system will be Inconsistent system
If 
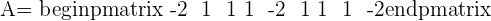
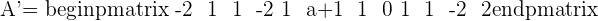
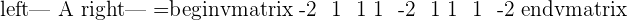
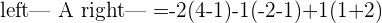
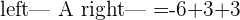
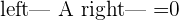
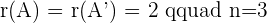 , hence the system is Consistent dependent system.
, hence the system is Consistent dependent system.
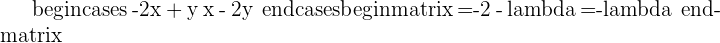
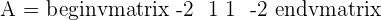
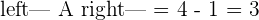
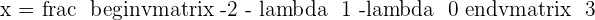
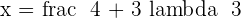
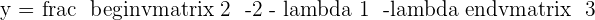
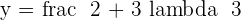
If 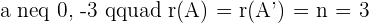 hence the system is a consistent independent system.
hence the system is a consistent independent system.
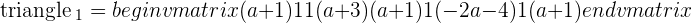
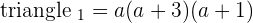
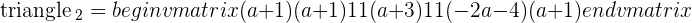
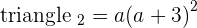
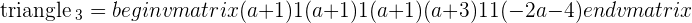
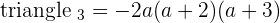
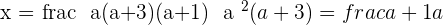
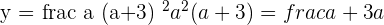
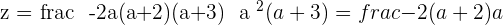
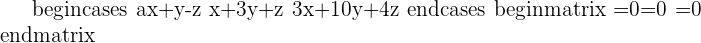
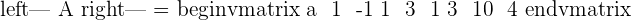
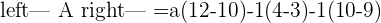
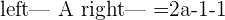
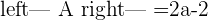
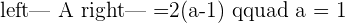
If 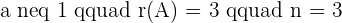
Trival solution: 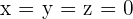
If 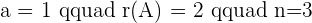
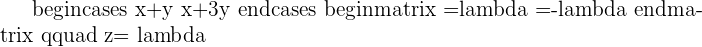
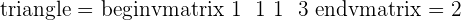
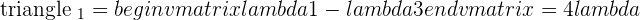
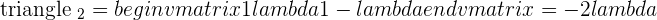
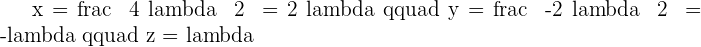
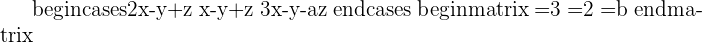
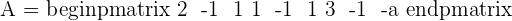
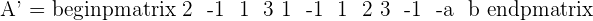
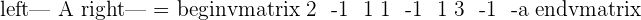
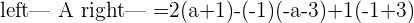
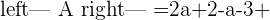
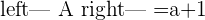
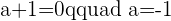
If 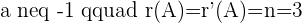 which means that the system will be a consistent independent system.
which means that the system will be a consistent independent system.
If 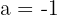
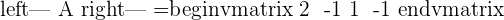
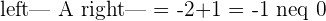
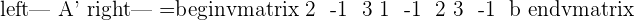
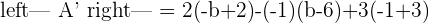
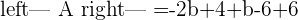
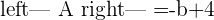
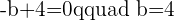
If 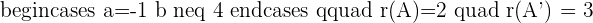
The above system will be an inconsistent system.
If 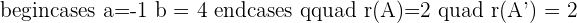
The above system will be a consistent dependent system.
See what you should look out for in a Math tutor near me.













I am impressed well done.