Chapters

What are Simultaneous Equations
You are already familiar with exponential equations. Exponential equations are used to model exponential growth and exponential decay. Exponential functions are the inverse functions of log functions. In this article, we will see what are simultaneous exponential equations. We will also learn to simultaneous exponential equations from some examples. So, let us first see what are simultaneous equations:
"Simultaneous equations have two or more unknown variables with a common value in each equation".
Simultaneous exponential equations are also known as a system of exponential equations. The word simultaneous implies that these equations are solved together. The values of unknown variables in one equation also satisfy the values for unknowns in the second equation. It means that the variables in one equation do not have a unique solution.
Before proceeding to simultaneous exponential equations, it is expected of you that you already know how to solve the system of linear equations. We know that in exponential equations, the independent variable is an exponent, i.e. 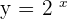 . In simultaneous exponential equations, the unknown variables are given in the exponent or power of the equations.
. In simultaneous exponential equations, the unknown variables are given in the exponent or power of the equations.
Strategies to Solve System of Exponential Equations
There are certain strategies to solve the system of exponential equations. These strategies are described below:
- Using a combination of methods like solving the system of linear equations and laws of exponents
- Solving the system as you solve a typical system of linear equations by elimination, substitution or comparison method
One should use the strategy according to the requirement of the equations. Remember that you can solve the system of exponential equations only if the bases of two or more exponential equations are the same. If the bases are the same, the exponential system of equations is solved simply by setting exponents on left and right hand side of the equations equal to each other.
However, there can be a situation where you are asked to solve the system of exponential equations with different bases. In this scenario, you should see if you can set the same bases for both the equations by applying the exponent rules.
Get more information Maths tuition here.
Examples
Let us solve the system of exponential equations in the following examples to clarify this topic further.
Example 1
Solve the system of exponential equations 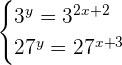
Solution
You can write the second equation as a cube of 3 on both the sides because 27 is equal to 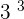 .
.
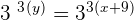
Multiplying the constant with terms inside the parenthesis will give us the following expression:
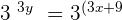
Hence, the system of exponential equations will be written as:
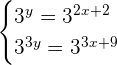
Since, the equations have same bases on the left and right side of the equations, so we can solve the exponents of this system by making them system of linear equations like this:
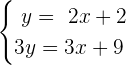
We can solve this system by substitution method. We already have  in the first equation, so we will substitute this value of
in the first equation, so we will substitute this value of  in the second equation like this:
in the second equation like this:
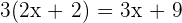
Solve the expression inside the parentheses on the left hand side of the equation:

Subtract  from both sides of the equation:
from both sides of the equation:
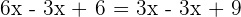

Subtract 6 from both sides of the equation to get the following expression:
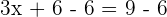
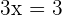
Divide both sides by 3 to get the value of 

Hence, we have obtained the value of  . Now, calculating the
. Now, calculating the  value has become easier because we can directly substitute
value has become easier because we can directly substitute  into the first equation to get the value of
into the first equation to get the value of  :
:



Hence, the solution of the above system of exponential equations is  and
and  . This solution set can be written as
. This solution set can be written as 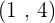 .
.
Verification
This step is not mandatory, however you can use this step to verify that your answer is true. Substitute  and
and  in the following system of exponential equations:
in the following system of exponential equations:
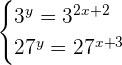
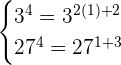
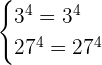
Hence, this shows that our solution is correct.
Example 2
Solve the following simultaneous exponential equations.

Solution
We can rewrite the second equation using the exponent product rule which says that product of two exponents with same base can be written as a single base with exponents added together and vice versa.

Suppose  and
and 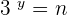 . The expression will be written like this:
. The expression will be written like this:
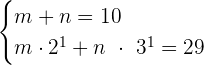
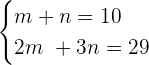
We can solve the above system of linear equations by elimination. Multiply the first equation by 2 to get the following expression:
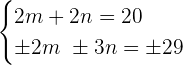
We will cancel 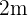 from the above system and the resultant expression will be:
from the above system and the resultant expression will be:
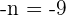
Multiply both sides by  to get
to get  .
.
Put this value of n in the first equation 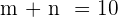 to get the following value for
to get the following value for  :
:
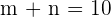
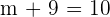
Subtract 9 from both the sides to get 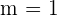
Now, we know the values of  and
and  . In the beginning we made the following assumptions about these two values:
. In the beginning we made the following assumptions about these two values:
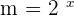 and
and 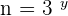
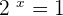 and
and 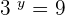
Since,  raised to the power
raised to the power  is equal to
is equal to  , i.e.
, i.e. 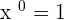 , so
, so  . Similarly,
. Similarly,  raised to a power 2 is equal to
raised to a power 2 is equal to  , i.e.
, i.e.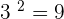 so,
so,  .
.
Hence, the solution set of the system of exponential equations is  .
.
Verification
We can verify our solution by putting the values of  and
and  variables into the system of exponential equations like this:
variables into the system of exponential equations like this:
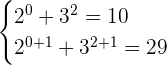
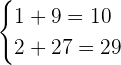
Hence, it is verified that our solution is correct.
Example 3
Solve the following system of exponential equations:
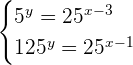
Solution
We can rewrite the first and second equations like this:
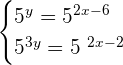
Write the exponents of the above system of exponential equations as system of linear equations like this:
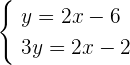
We can solve this system either by substitution or by elimination of variables. It is better to use elimination method because both the equations have  which can be eliminated smoothly:
which can be eliminated smoothly:
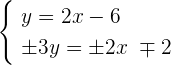
The resultant equation after elimination will be:
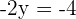
Multiply both sides of the above equation by -2 to make the variable positive:

Now, substitute this value of  in the second linear equation to get the value of
in the second linear equation to get the value of  .
.

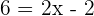
Add 2 to both the sides of the equation to get:
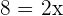
Divide both sides by 2 to get the value of  :
:

Hence, the value of  and
and  satisfy the system of exponential equations. Or in other words, we can say that
satisfy the system of exponential equations. Or in other words, we can say that 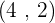 is the solution set of the original system of exponential equations.
is the solution set of the original system of exponential equations.
Verification
Let us verify our solution set by plugging in the values of  and
and  in the system of exponential equations like this:
in the system of exponential equations like this:
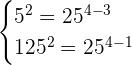

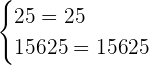
Hence, it is verified that 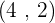 is the solution set of the system of exponential equations.
is the solution set of the system of exponential equations.
Example 4
Solve the following system of exponential equations:

Solution
We can write the first and second equations like this:
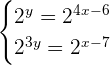
Write the exponents of the above system of exponential equations as system of linear equations like this:
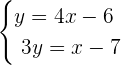
We can solve the above system of linear equation either by substitution or by elimination. Let us solve the system through substitution method. Substitute 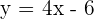 into
into 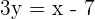 to get the following value of
to get the following value of  :
:

Solve the algebraic expression by multiplying 3 with ther term inside the parenthesis:
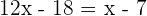
Subtract  from both the sides of the equation:
from both the sides of the equation:
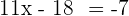
Add 18 to both sides of the equation to get the final value of  :
:
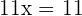
Divide both sides by  to get
to get 
Now, plug this value of  in the first equation
in the first equation 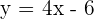

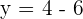

Hence, the value of  and the value of
and the value of  . In other words, we can say that the solution set of the system of exponential equation is
. In other words, we can say that the solution set of the system of exponential equation is  .
.
Verification
Now, we will verify our solution by plugging in the values of  and
and  in the original system of exponential equation:
in the original system of exponential equation:
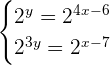
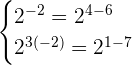
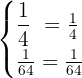
Hence, our solution set is true for the given system of exponential equations.
Example 5
Solve the following system of exponential equations.
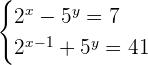
Solution
We can rewrite the second equation using the exponent product rule which says that product of two exponents with the same bases can be written as a single base with exponents added together and vice versa.

Suppose  and
and 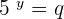 . Hence, the resultant system of exponential equations will be:
. Hence, the resultant system of exponential equations will be:

Apply the negative exponent rule to further simplify the above system of exponential equations. According to the negative exponent rule, the negative exponent in the numerator becomes positive in the denominator and vice versa.
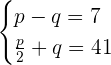
Multiply the second equation 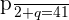 by 2 to get the following expression:
by 2 to get the following expression:

The first equation 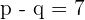 can be written as
can be written as 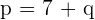 . Substitute this value of
. Substitute this value of 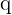 in the equation:
in the equation:
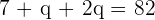
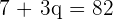
Subtract 7 from both sides of the equation to get:

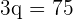
Divide both sides of the equation by 3 to get the value of 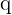 :
:
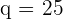
Substitute this value of 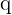 in the first linear equation
in the first linear equation 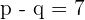 to yield the value of
to yield the value of  :
:
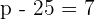
Add 25 to both sides of the equation:
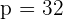
Now, we have got the values of  and
and 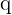 . Remember in the beginning of the problem, we made the following assumptions about these two values:
. Remember in the beginning of the problem, we made the following assumptions about these two values:
 and
and 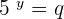
Putting the values of  and
and 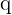 one by one in the equations will give us the values of
one by one in the equations will give us the values of  and
and  :
:
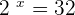
We know that  , so
, so  .
.
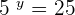
We know that  raised to a power 2 is equal to
raised to a power 2 is equal to  , so the value of
, so the value of  . Hence, the solution set of the above system of exponential equation is
. Hence, the solution set of the above system of exponential equation is 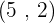 .
.
Verification
Let us verify our solution by putting the values of the variables in the original system of exponential equations.
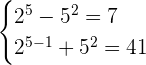
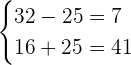
Hence, it is proved that our solution set is correct for the above system of exponential equations. Remember that you do not need to follow the verification step. This step is used only when you want to be confident that your solution set is true for the given system of exponential equations.
Summarise with AI:













I am impressed well done.