The word homogeneous means two or more than two things are the same or alike. This means that when we talk about homogeneous systems, they should be the same. The question is, what are the things that should be the same when we work with homogeneous systems? Is it the equation or something else? Keep on reading to find the answer.
Let's consider a system that has m number of equations and all the equations have n unknowns. To find either the system is homogeneous or not, we need to look at what is on the right-hand side of all those equations. If the right-hand side of all equations has zero independent terms that means the system is homogeneous. In easy words, if all the equations are equal to zero, we can call the system homogeneous. For example:

Take your time and think whether the above equation is homogeneous or not? If your answer is yes that means you can distinguish between a homogeneous equation and a non-homogeneous equation. Remember, number of equations and number of unknown variables doesn't matter, what matters is on the right-hand side. You can't call a system homogeneous if all the equations of that system are not equal to zero. The above system will have number of solutions but there is one solution which is obvious and that is:
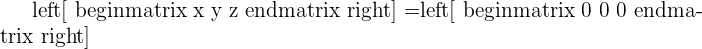
The other name of this solution is Trivial Solution. Trivial is a technical term that is commonly used in linear algebra. Basically, trivial is a solution set of a homogeneous system in which all the unknown have the value zero.

In the world of Linear Algebra, we don't focus on one solution instead, we focus on all possible outcomes. The most important part is to find whether the provided homogeneous system has a trivial solution or not. This means that a homogeneous system can have other solutions besides trivial. In short, a homogeneous system will have many solutions and they can be either trivial solution or non-trivial solutions (i.e. right-hand not equal to zero). However, in this article, we will only focus on a homogeneous system whose outcome is a trivial solution but don't forget, a homogeneous system can have multiple solutions and getting a trivial solution or not won't change the fact that the system is homogeneous or not. But the question is, how can a homogeneous system have multiple answers?
Boost your learning speed and understanding with a Maths tutor on Superprof.

Homogeneous System with Multiple Outcomes
In order to understand how a homogeneous system can have multiple answers, we have made a small example, let's consider the below equations:
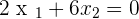
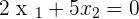
Without any doubt, the above equations belong to a homogeneous system. Subtract the second equation from the first equation and you will get a reminder of 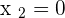 . If you substitute the value of
. If you substitute the value of  , you will find that the value of
, you will find that the value of 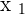 is also zero. Now this means that the outcome is a trivial solution.
is also zero. Now this means that the outcome is a trivial solution.
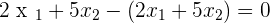

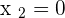
Plugging the value of  in the first equation:
in the first equation: 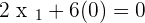
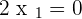

Hence, 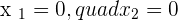
If we break the above equations into vectors (which would be like this: 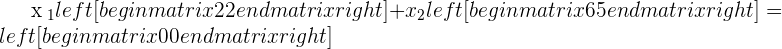 ), we can call it linearly independent. Always remember, linearly independent vectors will always have a trivial solution. Here is another homogeneous system:
), we can call it linearly independent. Always remember, linearly independent vectors will always have a trivial solution. Here is another homogeneous system:
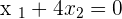

If we represent it as a vector then it will be something like this:  . Since the right side is equal to zero, there is no doubt that the system is homogeneous, however, will it result in only a trivial solution? No, because they are not linearly independent. You will get a trivial solution for sure but the above homogeneous system will have more than one solution (which means it will have other solutions including trivial solution). This non-trivial solution shows that the vectors are not linearly independent.
. Since the right side is equal to zero, there is no doubt that the system is homogeneous, however, will it result in only a trivial solution? No, because they are not linearly independent. You will get a trivial solution for sure but the above homogeneous system will have more than one solution (which means it will have other solutions including trivial solution). This non-trivial solution shows that the vectors are not linearly independent.
Check Superprof for different portfolios of maths tutors.
The necessary and sufficient condition for a homogeneous system has solutions other than the trivial (as mentioned above) when the rank of the coefficient matrix is less than the number of unknowns, that is to say, that the determinant of the coefficient matrix is zero.
r < n
Solving Homogeneous Systems
Q.1 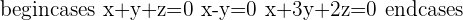
First of all, you need to place all the values in a matrix:
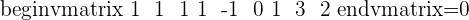
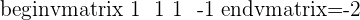
Now find the rank of the matrix as well as calculate the number of a number of unknowns:
The rank of the above matrix is: 
The number of unknowns are: 
Q.2 
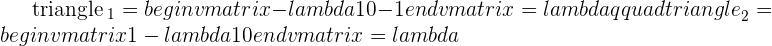
After solving the matrix, the value of x and y will be:
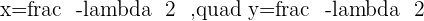
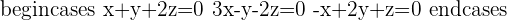

The rank of the above matrix is: 
The number of unknowns are: 
Trivial solution: 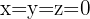
Q.4 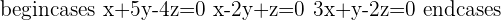
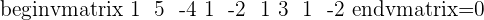
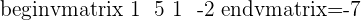
 The number of unknowns are:
The number of unknowns are: 
Q.5 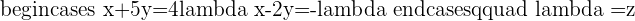

After solving the matrix, the value of x and y will be:
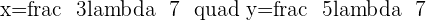
Q.6 

The rank of the above matrix is: 
The number of unknowns are: 
Trivial solution: 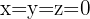
Find a Maths tutor on Superprof.













I am impressed well done.