When we talk about rational equations, one thing is for sure, you will see at least one rational expression. At this point, you might be wondering what does rational mean?
In the world of mathematics, a rational number is nothing but a fraction of two integers. It can be two variables as well, but you got the point of what rational means. For example, consider a point  . We call this number a decimal number because it contains a decimal. However, there is another way of writing this number like this
. We call this number a decimal number because it contains a decimal. However, there is another way of writing this number like this 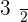 . If we divide
. If we divide  by
by  , you will get
, you will get  . That fraction is called a rational number because if you look closely, it is a fraction of two integers. Basically, a rational number means a number that can be written as a fraction or quotient of two variables or integers in a form of
. That fraction is called a rational number because if you look closely, it is a fraction of two integers. Basically, a rational number means a number that can be written as a fraction or quotient of two variables or integers in a form of 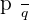 where q will always be a non-zero number.
where q will always be a non-zero number.
Now you know what a rational number means, here is a small question, can we say all numbers can be expressed as rational numbers? Take some time to think and don't forget what rational number means. If your answer is yes then congratulations! You understood the meaning of rational numbers. Let's take a number as an example, we picked the number  , how can you express it in rational form? Here is a possible way,
, how can you express it in rational form? Here is a possible way,  . No matter what number you choose, it always has a denominator like it always has a sign. No matter what number you pick whether it is a unit or million, it will still have a denominator and that is
. No matter what number you choose, it always has a denominator like it always has a sign. No matter what number you pick whether it is a unit or million, it will still have a denominator and that is  . In the above example, we showed you how all integers can be expressed as rational numbers. Here is another question to prove yourself, can be express decimal number as a rational number? Think about it.
. In the above example, we showed you how all integers can be expressed as rational numbers. Here is another question to prove yourself, can be express decimal number as a rational number? Think about it.

What is Rational Equations?
Like rational numbers, rational equations also exists. Rational equations works same as the rational number but with a slight change. Here is a representation of a rational equation 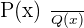 . Here
. Here  and
and  are polynomials. Whenever we deal with rational equations, we usually see this case
are polynomials. Whenever we deal with rational equations, we usually see this case 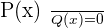 .
.
Solve rational equations by clearing the fractions by multiplying both sides of the equation by the least common denominator (LCD).
Solving Rational Equations
To solve rational equations, you need to find the least common multiple of the denominators of all polynomials. Once you find the least common multiple, you need to multiply it with both sides of the equation. Below is a practice question with its solution.

Considering the first term's denominator:
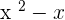
We can take x common from this denominator:
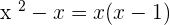
Now, you need to find the least common multiple of both denominators to solve this rational equation:
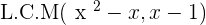
Always remember, the least common multiple should satisfy all polynomials
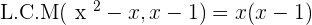
Now we have find the least common multiple, we need to check whether our both fraction's denominator can be converted to this least common multiple. There is no issue with the first term, however, the second term still needs to be converted. Let's pick up the second term and check what we can do to transform it.
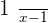
Multiplying numerator and denominator with x:
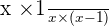
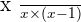
You can multiply numerator and denominator with any variable or number but don't forget that you need to multiply both side of the fraction. Let's continue solving the above equation.
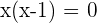


And hence, we found the factors which satisfy this equation "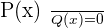 ". However, we are not done here, we need to verify our answers whether they are correct or not. Verifying the answers is very easy, all you need to do is to substitute the answers into the original equation.
". However, we are not done here, we need to verify our answers whether they are correct or not. Verifying the answers is very easy, all you need to do is to substitute the answers into the original equation.
Verifying the answers:

When  :
:

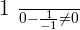
When  :
:



The equation has no solution because for  and
and  , the denominators are annulled.
, the denominators are annulled.
Examples
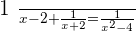


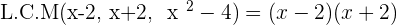
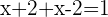

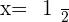
Verifying the answer:
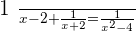
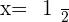
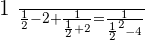
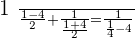
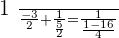

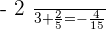
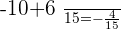
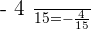
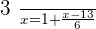
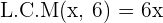
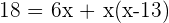

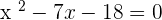

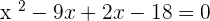
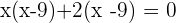



Verifying the answers:
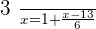
When  :
:
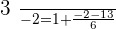




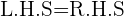
When  :
:
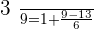
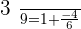
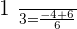
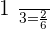

You can get a Maths tutor near me on Superprof.
Get information about maths tuition here.
Summarise with AI:













I am impressed well done.