Chapters
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 8
- Exercise 9
- Exercise 10
- Exercise 11
- Solution of exercise 1
- Solution of exercise 2
- Solution of exercise 3
- Solution of exercise 4
- Solution of exercise 5
- Solution of exercise 6
- Solution of exercise 7
- Solution of exercise 8
- Solution of exercise 9
- Solution of exercise 10
- Solution of exercise 11

Exercise 1
At a community meeting, there are double the number of women than men and triple the number of children than the total of men and women combined. How many men, women, and children are there if  people attend the meeting?
people attend the meeting?
Exercise 2
A barrel of oil has 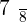 of its content removed. Then, it is filled with
of its content removed. Then, it is filled with  liters and the total content is
liters and the total content is 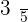 the capacity of the barrel. Calculate the total capacity of the barrel.
the capacity of the barrel. Calculate the total capacity of the barrel.
Exercise 3
A farm has pigs and turkeys. In total, there are  heads and
heads and  paws. How many pigs and turkeys are there on the farm?
paws. How many pigs and turkeys are there on the farm?
Exercise 4
Peter went on a road trip, during which time  liters of gasoline were consumed. However, he completed the trip in two stages. In the first, he consumed
liters of gasoline were consumed. However, he completed the trip in two stages. In the first, he consumed  of the gasoline that was in the tank and in the second stage, half of the gasoline that he had left in the tank.
of the gasoline that was in the tank and in the second stage, half of the gasoline that he had left in the tank.
1. Determine the number of liters of gasoline that were in the tank before the trip.
2. Determine the number of liters consumed at each stage.
Exercise 5
In a bookstore, Anne buys a novel with a third of her money and a comic with two-thirds of what remained. When she left the bookstore, she had  dollars. How much money did Anne have before arriving at the store?
dollars. How much money did Anne have before arriving at the store?
Exercise 6
A clock sounds to indicate the time of 3 o'clock. At what time between  and
and  will the hour and minute needles overlap?
will the hour and minute needles overlap?
Exercise 7
A clock sounds to indicate the time of 2 o'clock. At what time will its needles form a right angle for the first time?
Exercise 8
A truck leaves a city at a speed of  mph. An hour later, a car leaves the same city and travels in the same direction at a speed of
mph. An hour later, a car leaves the same city and travels in the same direction at a speed of  mph.
mph.
1. How many hours after leaving the city will the car reach the truck?
2. What is the distance from the city where the car will reach the truck?
Exercise 9
At 9 a.m., two cyclists simultaneously leave their houses and travel towards each other on the same road. Houses A and B are located 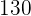 miles away from each other. If the cyclist who leaves from House A pedals at a constant speed of
miles away from each other. If the cyclist who leaves from House A pedals at a constant speed of  mph, and the cyclist who leaves from House B travels at
mph, and the cyclist who leaves from House B travels at  mph, how far from House A will the two meet and at what time?
mph, how far from House A will the two meet and at what time?
Exercise 10
A faucet takes  hours to fill a water tank, and another faucet takes four hours to fill a tank of the same size. How long will it take to fill a tank of the same size if both faucets are distributing water together into the same tank?
hours to fill a water tank, and another faucet takes four hours to fill a tank of the same size. How long will it take to fill a tank of the same size if both faucets are distributing water together into the same tank?
Exercise 11
A golden brick of 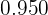 purity weighs
purity weighs 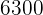 grams. What amount of pure copper should be added to lower its purity to
grams. What amount of pure copper should be added to lower its purity to  ?
?
Find the best maths tutor on Superprof.
Solution of exercise 1
At a community meeting, there are double the number of women than men and triple the number of children than the total number of men and women combined. How many men, women, and children are there if  people attend the meeting?
people attend the meeting?
Men: 
Women: 
Children: 
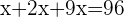
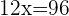

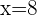
Men: 
Women: 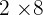 =
= 
Children: 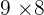 =
= 
Solution of exercise 2
A barrel of oil has 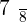 of its content removed. Then, it is filled with
of its content removed. Then, it is filled with  liters and the total content is
liters and the total content is 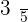 the capacity of the barrel. Calculate the total capacity of the barrel.
the capacity of the barrel. Calculate the total capacity of the barrel.
Let the total volume of the barrel equal to "x".
The first step is to deduct the 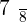 from the total amount.
from the total amount.
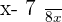

The next step is to add the  liters which will equal to
liters which will equal to 

After talking LCM: 

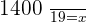
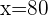
Find various learn Maths online on Superprof.
Solution of exercise 3
A farm has pigs and turkeys. In total, there are  heads and
heads and  paws. How many pigs and turkeys are there on the farm?
paws. How many pigs and turkeys are there on the farm?
Let the number of pigs = 
Turkeys = 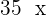
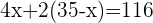
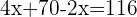


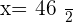
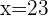
Pigs = 
Turkeys = 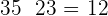
Check Superprof for different portfolios of maths tutors.
Solution of exercise 4
Peter went on a road trip, during which time  liters of gasoline were consumed. However, he completed the trip in two stages. In the first, he consumed
liters of gasoline were consumed. However, he completed the trip in two stages. In the first, he consumed  of the gasoline that was in the tank and in the second stage, half of the gasoline that he had left in the tank.
of the gasoline that was in the tank and in the second stage, half of the gasoline that he had left in the tank.
1. Determine the number of liters of gasoline that were in the tank before the trip.
First stage. 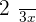
Second stage. 
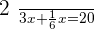
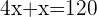
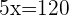

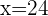
2. Determine the number of liters consumed at each stage.
First stage: 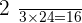
Second stage: 
Solution of exercise 5
In a bookstore, Anne buys a novel with a third of her money and a comic with two-thirds of what remained. When she left the bookstore, she had  dollars. How much money did Anne have before arriving at the store?
dollars. How much money did Anne have before arriving at the store?
Let the total amount that Anne had equal to "x"
Cost of novel = 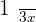
Cost of comic = 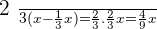
The remainder cost = 
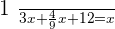
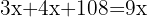

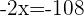

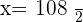
 dollars
dollars
Solution of exercise 6
A clock sounds to indicate the time of 3 o'clock. At what time between  and
and  will the hour and minute needles overlap?
will the hour and minute needles overlap?
Keep in mind that the angle or arc representing the minute hand's position is always  times greater than the arc that describes the hour hand.
times greater than the arc that describes the hour hand.
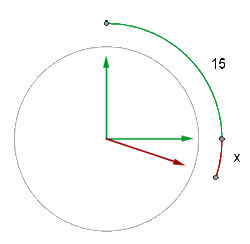
x is the arch that describes the needle hourly.
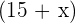 is the arch that describes the minute hand.
is the arch that describes the minute hand.
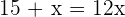


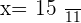
The needles will overlap at  and
and  seconds.
seconds.
Solution of exercise 7
A clock sounds to indicate the time of 2 o'clock. At what time will its needles form a right angle for the first time?
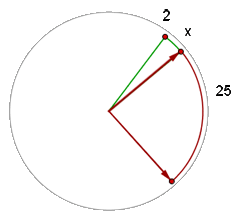
Turning clockwise, the needles will form a right angle approximately at  . Therefore, let x be the arc that describes the hour needle.
. Therefore, let x be the arc that describes the hour needle.
x is the arc that describes the hour needle.
 , is the arc that describes the minute hand.
, is the arc that describes the minute hand.
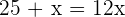
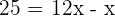
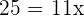
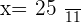
The clock will form a 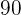 angle at
angle at  and
and  seconds.
seconds.
Solution of exercise 8
A truck leaves a city at a speed of  mph. An hour later, a car leaves the same city and travels in the same direction at a speed of
mph. An hour later, a car leaves the same city and travels in the same direction at a speed of  mph.
mph.
1. How many hours after leaving the city will the car reach the truck?
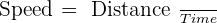

Distance traveled by car = 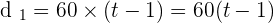
Distance traveled by truck = 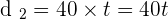
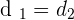
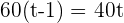
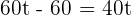
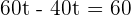
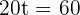
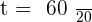
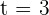
As the car leaves the city one hour later than the truck, the time it will take to reach the truck will be  hours.
hours.
2. What is the distance from the city where the car will reach the truck?

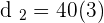
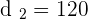 miles
miles
Solution of exercise 9
At 9 a.m., two cyclists simultaneously leave their houses and travel towards each other on the same road. Houses A and B are located 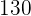 miles away from each other. If the cyclist who leaves from House A pedals at a constant speed of
miles away from each other. If the cyclist who leaves from House A pedals at a constant speed of  mph, and the cyclist who leaves from House B travels at
mph, and the cyclist who leaves from House B travels at  mph, how far from House A will the two meet and at what time?
mph, how far from House A will the two meet and at what time?
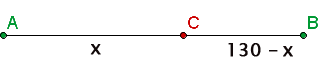
The cyclist travels at  mph from house A and his friend travels at
mph from house A and his friend travels at  mph from house B. They will meet up at a certain place and we will call that place C. If we add the distance of AC and CB, we know that their sum will be
mph from house B. They will meet up at a certain place and we will call that place C. If we add the distance of AC and CB, we know that their sum will be 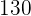 (because that is the overall distance). To find those distances, we will use speed formula since we know the speed and we will assume that at "t", they will meet each other.
(because that is the overall distance). To find those distances, we will use speed formula since we know the speed and we will assume that at "t", they will meet each other.
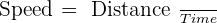

Distance traveled by the cyclist from house A = 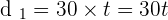
Distance traveled by the cyclist from house B = 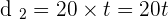
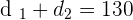
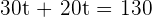


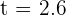 hours
hours
Let's convert 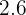 hours into hour:min
hours into hour:min
 minutes
minutes
time =  hour and
hour and  minutes
minutes
They will meet at 11:36 am.
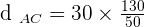
 miles
miles
Solution of exercise 10
A faucet takes  hours to fill a water tank, and another faucet takes four hours to fill a tank of the same size. How long will it take to fill a tank of the same size if both faucets are distributing water together into the same tank?
hours to fill a water tank, and another faucet takes four hours to fill a tank of the same size. How long will it take to fill a tank of the same size if both faucets are distributing water together into the same tank?
In one hour the first faucet fills 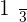 of the tank.
of the tank.
In one hour the second faucet fills  of the tank.
of the tank.
In one hour two together faucets will have filled:
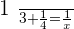
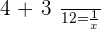


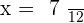 hours
hours
Solution of exercise 11
A golden brick of 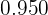 purity weighs
purity weighs 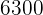 grams. What amount of pure copper should be added to lower its purity to
grams. What amount of pure copper should be added to lower its purity to  ?
?
| Gold | Copper | Total | |
|---|---|---|---|
| No. of g | 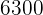 |  |  |
| Pure Gold |  | 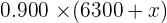 |


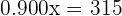

Copper  grams
grams
You can get a Maths tutor near me on Superprof.
Summarise with AI:













I am impressed well done.