Chapters
Exercise 2
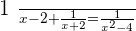
Exercise 3
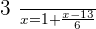
Exercise 4
Exercise 5
Two taps A and B fill a swimming pool together in two hours. Alone, it takes tap A three hours less than B to fill the same pool. How many hours does it take each tap to fill the pool separately?
Exercise 6
A faucet takes more than two hours longer to fill a tank than it would with a second faucet working at the same time as the first, where the job can be completed in 1 hour and 20 minutes. How long does it take to fill each one separately?
Solution of exercise 1
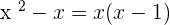
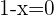
Verifying the solution:
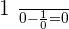
The equation has no solution because for x = 1, the denominators are annulled.
Solution of exercise 2
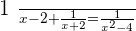
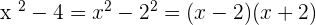
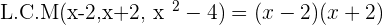
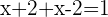
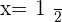
Verifying the answer:
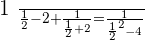
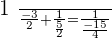
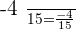
Solution of exercise 3
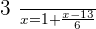
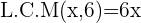
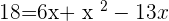
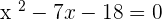
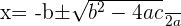
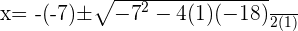
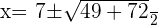
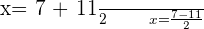
Verifying the answer:
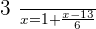
For 
:
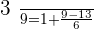
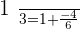
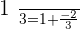
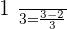
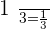
For 
:
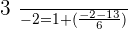
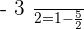
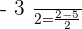
Solution of exercise 4
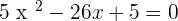
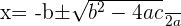
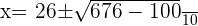
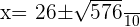
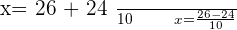
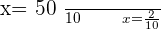
Verifying the answer:
When 
:
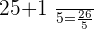
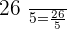
When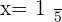 
:
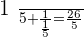
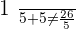
Solution of exercise 5
Two taps A and B fill a swimming pool together in two hours. Alone, it takes tap A three hours less than B to fill the same pool. How many hours does it take each tap to fill the pool separately?
Time of A = 
Time of B = 
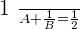
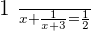
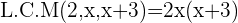
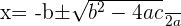
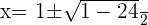
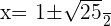
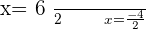
Verifying the answers:
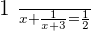
When 
:
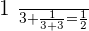
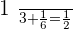
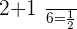
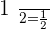
When :
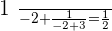
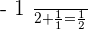
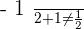
Time of A 3 hours
Time of B 6 hours
Solution of exercise 6
A faucet takes more than two hours longer to fill a tank than it would with a second faucet working at the same time as the first, where the job can be completed in 1 hour and 20 minutes. How long does it take to fill each one separately?
1st Time =
2nd Time =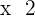 
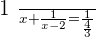
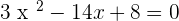
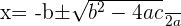
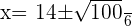
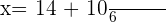x=\frac { 14 - 10}{ 6 } 
x=\frac { 24 }{ 6 } \qquad 
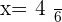
1st Time 4 hours
2nd Time 2 hours
not a solution because the time for the second faucet would be negative.
You can get a Maths tutor near me on Superprof.
Get information about maths tuition here.
Did you like this article? Rate it!
Loading...
I am impressed well done.