Chapters
In this article, you will learn what are quadratic equations, the properties of their roots, how to represent them graphically, and how to solve them using the three methods with examples. So, let us get started.

What are Quadratic Equations?
The standard form of a quadratic equation is given below:
 , where
, where 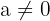
Here a is the leading coefficient of the equation and it should not be zero. The values of x that make the equation true are known as zeroes or roots of a quadratic equation. You can see that the quadratic equation is a second degree polynomial which means that the highest degree of this equation is 2.
Properties of Roots of a Quadratic equation
- If c = 0, then one of the roots of a quadratic function is zero and the other is equal to
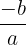
- If b and c are equal to zero, then both the roots of a quadratic function are zero
- If a is equal to c, then both the roots of the function are reciprocal to each other
Graphical Representation of the Quadratic equations
- The sign of the leading coefficient "a" determines the shape of the graph of quadratic functions. If the value of "a" is greater than 0, i.e. it is positive, then the parabola opens upwards.
- If the leading coefficient "a" is less than 0, i.e. it is negative, then the parabola opens downwards.
- The maximum or minimum (depending upon the shape of the parabola) point of the parabola is known as a vertex. A line that vertically passes through the vertex is known as the axis of symmetry.
- The points where the parabola intersects the x-axis are known as x-intercepts of the function. These x-intercepts are the roots or zeros of the function.
Find the best maths tutor on Superprof.
Methods for Solving Quadratic Equations
i. Factoring
It is the simplest way to find the roots of the quadratic functions. All we have to do is expand the middle term to get four terms, group the like terms and factor them. The following steps are generally involved in this process:
- All the terms are taken on the left-hand side of the equation. The equation is set to zero.
- Expand the middle term into two terms in such a way that the product of two terms is equal to
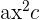 and the sum or difference of two terms is equal to
and the sum or difference of two terms is equal to 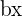 .
. - Group the like terms and find factors.
- Set each factor equal to zero and solve the new equations for the unknown variable x.
- You can also substitute the value of x in the original equation to check whether it satisfies the equation or not.
Example
Solve  by factoring.
by factoring.
Solution
You can see that the constant is on the right hand side of the equation. Hence, we will bring it to the left hand side of the equation and set the equation equal to zero.
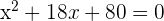
Now, we will expand the middle term into two terms in such a way that the product is equal to  and sum or difference is equal to
and sum or difference is equal to 
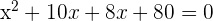

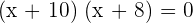
We got two new equations by setting each factor equal to zero. We will solve the two equations separately for x:
 and
and 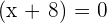
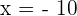 and
and 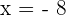
Hence -10 and -8 are the roots of the equation. To check our answer, we will substitute these values in the original equation:
 at
at 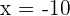
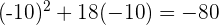
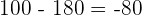
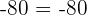
 at
at 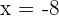
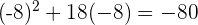

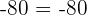
Hence, it is proved that our answer is correct, i.e, -10 and -8 are the solutions to the equation.
ii. The Quadratic Formula
Most of the time we cannot find factors of a quadratic equation. In these problems, using the quadratic formula helps us to determine the roots or zeroes of the equation. We especially use the quadratic formula when the roots or zeroes of the quadratic equations are not rational numbers. The following formula is used for a quadratic equation  ,
,
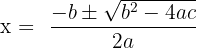
The element of the formula present under the radical sign  is called the discriminant. The discriminant of the quadratic formula determines the following three possibilities:
is called the discriminant. The discriminant of the quadratic formula determines the following three possibilities:
- Two different roots are obtained if the discriminant
 is a positive number.
is a positive number. - A function has only one real root, zero or solution if the discriminant
 is zero.
is zero. - A function has no real solution if the discriminant
 is less than 0, i.e. it is a negative number.
is less than 0, i.e. it is a negative number.
Example
Find the roots of the equation 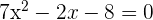
Solution
We cannot factorize the equation in this example, therefore we will move forward to use the quadratic formula to find the roots of the equation:
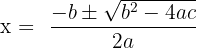
Here, a = 7, b = -2 and c = -8.
We will substitute the values of a, b and c in the formula:
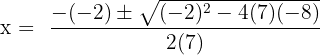
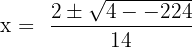
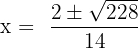
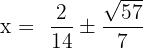
Simplify the above expression to get the following solutions:
 and
and 
You can check for a maths tutor here.
iii. Completing the Square
The third method of solving the quadratic equations is completing the square method. If the roots of the equation are real of imaginary numbers, then this method is the most suitable one. The following steps are involved in solving the quadratic equations through this method:
- Take constant on the right-hand side of the equation to convert the equation into the form

- The leading coefficient "a" should be equal to 1. If it is not the case then you should make it equal to 1 by dividing the entire equation by the leading coefficient a.
- Use the value of b to make a perfect square on the left-hand side of the equation. Add
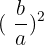 to both sides of the equation.
to both sides of the equation. - In the last step, take the square root on both sides of the equation and solve the resulting equation for unknown value x.
Find various learn Maths online on Superprof.
Example
Solve the equation 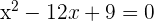 using completing the square method.
using completing the square method.
Solution
Take the constant on the right hand side of the equation:

Calculate the value of 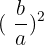 and add it to both sides of the equation:
and add it to both sides of the equation:
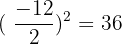
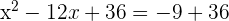
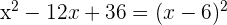
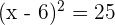
Take square root of both sides of the equation and solve the resulting equation for x:
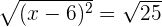
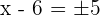
 or
or 
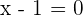 or
or 
 or
or 
Summarise with AI:













I am impressed well done.