Chapters
If you are here that means you know what an equation means. There are infinite equations in this world. It would take us a long time to understand them unless we categorize them. That is why mathematicians categorized equations in different types so that they are easier to understand. The biggest advantage of the categorization of equations is that we can easily tackle with them. Once we find the type of the equation, we can easily solve them to find roots or solutions. For example, if you see an equation like this 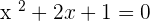 , the first thing you will do is to understand the equation. You know it is a quadratic equation and the next thing you will think is how to solve this quadratic equation? By means of middle term breaking or the quadratic formula. Well, this is a story for another blog but we know you must be wondering what is a quadratic equation? Keep on reading to find out.
, the first thing you will do is to understand the equation. You know it is a quadratic equation and the next thing you will think is how to solve this quadratic equation? By means of middle term breaking or the quadratic formula. Well, this is a story for another blog but we know you must be wondering what is a quadratic equation? Keep on reading to find out.
Check for outstanding maths tutors near me here.

1. Polynomial Equations
Polynomial equations are in the form P(x) = 0, where P(x) is a polynomial. These types of equations are also known as equivalent equations because both sides of the equation have the same solution. In addition, there can be more than one unknown in the equation. The word poly means more than one and nomial means number of terms. There are three types of polynomial equations.
Types of Polynomial Equations
1.1 Linear Equations
Linear equations are equations of the type 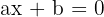 , with
, with 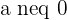 , or any other equation in which the terms can be operated and simplified into an equation of the same form. For example:
, or any other equation in which the terms can be operated and simplified into an equation of the same form. For example:
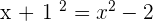
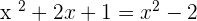
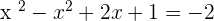
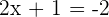
Introducing 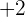 on both sides of the equation:
on both sides of the equation:
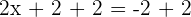


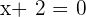
The graph of a linear equation will always be a straight line. The degree of linear equation will always be  .
.
1.2 Quadratic Equations
Quadratic equations are equations of the type 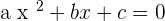 , with
, with 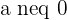 . A Quadratic equation will always have 2 roots. You can even convert other equations into the quadratic equations, we call them "biquadratic equations". If you draw a graph of a quadratic equation, you will find that the graph is a U-shape graph. The graph will always have either a maximum point or minimum and the same point is also known as the point of symmetry. This means that at that point if you merge both sides, they will overlap each other. The degree of the quadratic equation will always be
. A Quadratic equation will always have 2 roots. You can even convert other equations into the quadratic equations, we call them "biquadratic equations". If you draw a graph of a quadratic equation, you will find that the graph is a U-shape graph. The graph will always have either a maximum point or minimum and the same point is also known as the point of symmetry. This means that at that point if you merge both sides, they will overlap each other. The degree of the quadratic equation will always be  .
.
Get information about maths tuition in the UK.
1.3 Polynomial Equation
At this point, you must be wondering that we are studying polynomial and how come a polynomial has a type that has the same name "polynomial"? If an equation is nether a linear or quadratic, we call that equation polynomial. For example, 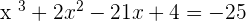 , this type of equation is a polynomial equation. The degree of these types of equations will always be greater than
, this type of equation is a polynomial equation. The degree of these types of equations will always be greater than  . Cubical as well as the quartic equation is a type of polynomial equation.
. Cubical as well as the quartic equation is a type of polynomial equation.
Incomplete quadratic equations
Incomplete equation are a type of quadratic equation. If the value of b or c (in some cases, even both) are equal to zero, the resultant equation will be an incomplete equation. Below are some examples of incomplete equations:
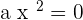

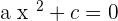
Solving incomplete equations is very easy and does not require advanced maths (or different formulas) to solve.
1.3 Cubic Equations
Cubic equations are equations of the type  , with
, with 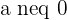 . The degree of cubic equation will always be
. The degree of cubic equation will always be  .
.
1.4 Quartic Equations
Quartic equations are equations of the type  ,
, 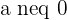 . In addition, the polynomial degree of the quartic equation will always be
. In addition, the polynomial degree of the quartic equation will always be  .
.
Biquadratic Equations
Biquadratic equations are quartic equations that do not have terms with an odd degree. Basically, they are high polynomial degree equation but they are converted to the quadratic equation which makes it easier to solve.
 , with
, with 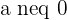 .
.
2. Rational Polynomial Equations
The rational polynomial equations are of the form  , where
, where  and
and  are polynomials. The word rational means ratio which means rational polynomial equations will always be in fraction. In addition,
are polynomials. The word rational means ratio which means rational polynomial equations will always be in fraction. In addition,  and
and  will not be equal to zero.
will not be equal to zero.

3. Irrational Polynomial Equations
The irrational equations are those that have at least a polynomial under the radical sign.
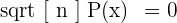
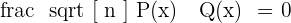

4. Transcendental Equations
The transcendental equations are equations that include transcendental functions.
4.1 Exponential Equations
Exponential equations are equations in which the unknown appears in the exponent.
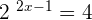

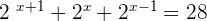
4.2 Logarithmic Equations
Logarithmic equations are equations in which the unknown is affected by a logarithm.


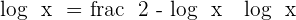
4.3 Trigonometric Equations
Trigonometric equations are the equations in which the unknown is affected by a trigonometric function.
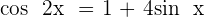

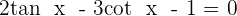
Learn more from Maths tutors near me on Superprof.













I am impressed well done.