Chapters

Exercise 2

Exercise 3
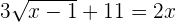
Exercise 4

Exercise 5
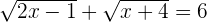
Solution of exercise 1


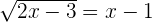
Taking square on both sides:
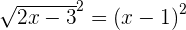
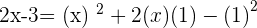
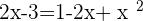


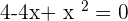

You can solve the above equation with the help of middle term breaking or by using the quadratic formula. We will be using the quadratic formula in this question:
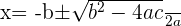
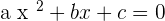



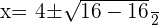
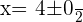



Solution of exercise 2

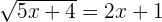
Taking square on both sides:


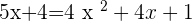
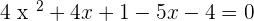
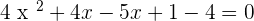
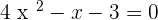
You can solve the above equation with the help of middle term breaking or by using the quadratic formula. We will be using the middle term breaking method in this question:
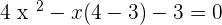
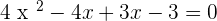
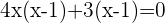
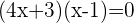

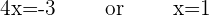

Substituting the values of x in the original equation to verify answers:

When  :
:


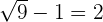
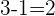
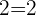
LHS=RHS, hence  is a valid answer
is a valid answer
When  :
:
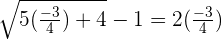

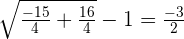



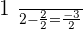
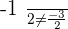
Hence,  is not a valid answer.
is not a valid answer.
Solution of exercise 3
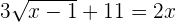

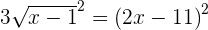
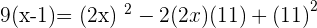
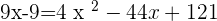

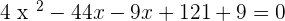

Using the quadratic formula to find the roots of the above equation:
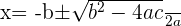
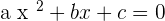

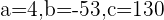
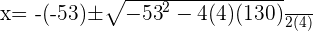
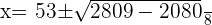
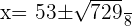
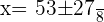




Verifying the above answers:
When 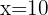 :
:
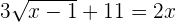




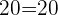
L.H.S=R.H.S
When  :
:
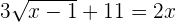
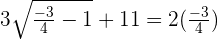
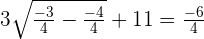
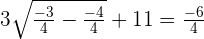
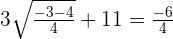
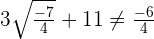
Hence, 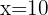 is the only valid answer.
is the only valid answer.
Solution of exercise 4

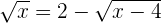
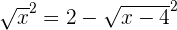




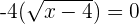
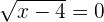
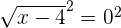

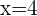
Verifying the answer:

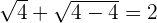

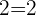
L.H.S=R.H.S
Solution of exercise 5
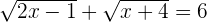
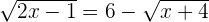


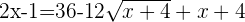

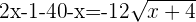





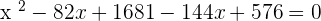
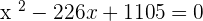
Using the breaking the middle term method to find the roots of the above equation:
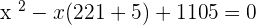
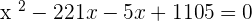
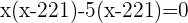



Verifying both answers:
When  :
:
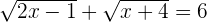
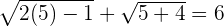
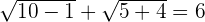

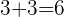
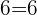
R.H.S=L.H.S
When  :
:
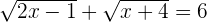



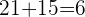
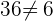
Hence,  is the only valid answer.
is the only valid answer.
Summarise with AI:














I am impressed well done.