Chapters
Working with one or two linear equations isn't a big deal. However, if you are working with a lot of linear equations, let's say four or five, then there are some changes. Whenever we deal with a lot of linear equation, we call it a system of equation. In simple words, a system of equations means that a set of equations that you work with all together. Linear equations are simple to understand as well as to solve. On the other hand, dealing with a lot of linear equations might be difficult and that is why we use numerical methods to estimate the solutions of a specific system.

What is a Linear Equation?
If you are working with linear equations, it is necessary for you to understand what linear equation means. Often people don't know what linear equation means. The word "Linear" tells a straight line and hence linear equation means straight line's equation. If the line is not straight that means it is not a linear equation, it can be the quadratic or polynomial equation. Always remember, linear equations will always have straight lines otherwise they are not linear equations.
Linear Equation with "n" Unknowns
When you look at a linear equation, you will most see two things. One is the variable and the other is the constant. The variable will ALWAYS be a 1st-degree polynomial. That is another condition of the linear equation. If your specific system has an equation that doesn't have a polynomial degree equal to one that means your system isn't a linear system.
It is any expression such as: 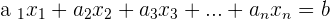 , where
, where  .
.
Where, 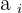 , are the coefficients,
, are the coefficients,  , the independent term, and
, the independent term, and 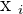 , the unknowns.
, the unknowns.
Solution of a Linear Equation
Any set of n real numbers that verify the equation is called a solution to the equation.
Given the equation 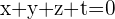 , the solutions to it are:
, the solutions to it are:

Equivalent Equations
Equivalent equations are those equations that have the same solution. In other words, algebraic equations that have identical roots are called equivalent equations. There are some reasons that result in an equivalent equation. The first one is adding or subtracting the same expression or number to both sides of an equation. The second one is the multiplication or division of a non-zero number to an equation's both sides.
Check Superprof for different portfolios of maths tutors.
Systems of Linear Equations
It is a set of algebraic expressions in the form:

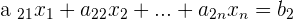
.....................................................................

Where:
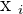 are the unknowns,
are the unknowns, 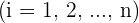 .
.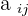 are the coefficients,
are the coefficients, 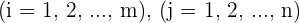 .
. are the independent terms,
are the independent terms, 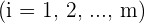 .
. ;
;  or
or 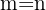 or
or 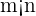
- Note that the number of equations need not equal the number of unknowns.
-
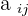 and
and  .
. - When n takes a low value, it is usual to designate the unknowns with the letters x, y, z, t, ...
- When
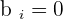 , for all i, the system is called homogeneous.
, for all i, the system is called homogeneous.
Find the best maths tutor on Superprof.
Solution of a System
It is each set of values that satisfies all equations. Linear lines intersect each other at a point. In a few cases, linear lines intersect each other at different points. These points of intersection are known as solution of a system.
Equivalent Systems of Equations
Equivalent equation systems have the same solution, although they may have different numbers of equations. Equivalent systems of equations are obtained by elimination if:
- All coefficients are zeros.
- Two rows are equal.
- A row is proportional to another.
- A row is a linear combination of others.
Equivalence Criteria
There are some criteria that you should know. Below are the equivalence criteria:
- If both members of an equation of a system are added or subtracted by the same expression, the resulting system is equivalent.
- If both members of the equations of a system are multiplied or divided by a number other than zero, the resultant system is equivalent.
- If an equation of a system is added or reduced by another equation of the same system, the resultant system is equivalent.
- If an equation in a system is replaced by another equation that results from adding the equations of a system previously multiplied or divided by nonzero numbers, the resultant system is equivalent.
- If the order of the equations or the order of the unknowns of a system is changed, it is another equivalent system.
Types of System
There are different types of system that has different outcomes. Before we start to work on a system, we usually check what kind of system we are dealing with. Basically, systems might look the same but what differs is the result of that system (i.e. number of a specific system's solution). Below are some types of system that you should be aware of:
Inconsistent
This type of system has no solution. This means that all the linear lines in that system don't meet up with each other.
Consistent
Consistent system means that a specific system has at least one solution. However, there are two types of consistent systems.
Consistent independent
Consistent independent system will always have a single solution. This means that linear lines meet up at a single point.
Consistent dependent
This is the second type of consistent system which means that a specific system will have an infinite number of solutions. Imagine 2 lines system, both lines overlap each other. This means that there will be a lot of solutions of that specific system. That is why we say that the system has an infinite number of solutions.
System of Linear Equations in Triangular Form
They are a system of equations that have an unknown less in each equation than the equation previously.
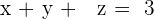
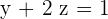
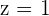
In the 3rd equation, there is 
Substituting this value into the 2nd equation, it becomes  .
.
And substituting this into the 1st equation, it becomes  .
.
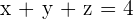
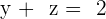
With this system, there are more unknowns than there are equations. In this case, take one of the unknowns (eg z) and change its member.
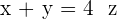

Consider 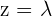 , with
, with 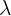 being a parameter to take any real value.
being a parameter to take any real value.


The solutions are:

You can get a Maths tutor near me on Superprof.













I am impressed well done.