Chapters
In this article, we will discuss the methods that are used to find the solutions to quadratic equations and the properties of the solutions to quadratic equations. The general form of a quadratic equation is  . The solutions to quadratic equations are known as roots or zeroes of the equation.
. The solutions to quadratic equations are known as roots or zeroes of the equation.
We can solve quadratic equations using three methods such as factoring, the quadratic formula, and completing the square. Let us discuss each of the methods one by one with examples.

Factoring
Follow these steps to solve a quadratic equation by factoring:
- Take all the terms of the quadratic equation on one side and put zero on the other side of the equation
- Expand the middle term in such a way that its product is equal to ac and sum or difference is equal to the middle term.
- In the next step, factor the equation and set each factor equal to zero
- After setting each factor equal to zero, you will get two new equations. You need to solve each of the equations to get the values of the variable.
- In the last step of this process, you can substitute the value of the variable in the original equation to check whether your answer is correct or not. This is not a mandatory step.
Now, we will see how to solve quadratic equations using factoring through the following examples.
Example 1
Solve 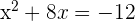 by factoring.
by factoring.
Solution
First, we will bring the constant on the left-hand side of the equation and set the equation equal to zero like this:
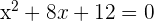
Now, we will factor the equation like this:



By setting each factor equal to zero, we will get two equations:
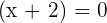 and
and 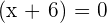
 and
and 
Hence, the roots or zeroes of the equation are -2 and -6. Now, we will substitute them in the original equation to see whether our answer is correct or not.
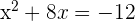 at
at 
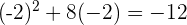
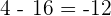
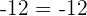
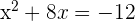 at
at 
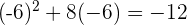
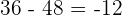
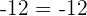
Hence, it is proved that -2 and -6 are solutions to the original equation.
Example 2
Solve 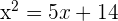 by factoring.
by factoring.
Solution
First, we will bring all the terms to the left hand side of the equation and set the equation equal to zero like this:
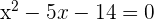
Now, we will factor the equation like this:

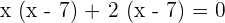

By setting each factor equal to zero, we will get two equations:
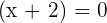 and
and 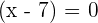
 and
and 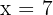
Hence, the roots or zeroes of the equation are -2 and -6. Now, we will substitute them in the original equation to see whether our answer is correct or not.
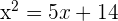 at
at 



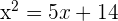 at
at 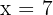

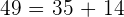
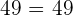
Since by substituting the values in the original equation satisfy the equation, so it is proved that -2 and 7 are solutions to the original equation.
Find the best Maths tutor on Superprof.
The Quadratic Formula
Some quadratic equations cannot be solved by factoring. This happens especially when the solutions of the quadratic equation are not rational numbers. In these cases, you can employ the quadratic formula to find the solutions to the quadratic equation.
For a quadratic equation  , we use the following formula to find the solution:
, we use the following formula to find the solution:
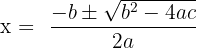
Remember that the part of the formula under the radical sign  is known as discriminant and it determines the three possibilities. These three possibilities are:
is known as discriminant and it determines the three possibilities. These three possibilities are:
- You can get two distinct real roots of the equation if the discriminant
 is a positive number.
is a positive number. - You will get one real root or solution if the discriminant
 is equal to zero.
is equal to zero. - You will get no real solution to the equation if the discriminant
 is a negative number.
is a negative number.
Now, let us solve some quadratic equations through the quadratic formula.
Example 1
Find the roots of the equation 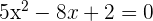
Solution
This equation cannot be solved through factoring, hence we will use the following quadratic formula to find the roots of the equation:
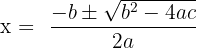
Here, a = 5, b = -8 and c = 2.
We will substitute the values of a, b and c in the formula:
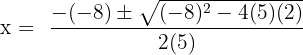
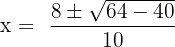
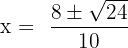
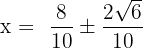
By simplifying the above expressions, we will get the following answers:
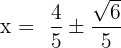
We can write the answers in decimal form by solving the above expression like this:
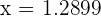 and
and 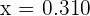
Example 2
Find the roots of the equation 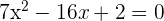
Solution
This equation cannot be solved through factoring, hence we will use the following quadratic formula to find the roots of the equation:
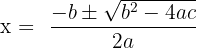
Here, a = 7, b = - 16 and c = 2.
We will substitute the values of a, b and c in the formula:
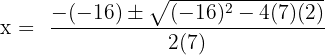
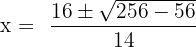
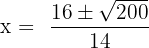
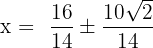
By simplifying the above expressions, we will get the following answers:
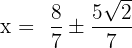
We can write the answers in decimal form by solving the above expression like this:
 and
and 
Find more learn Maths online here on Superprof.
Completing the Square
Another method to solve a quadratic equation is completing the square method. This method is suitable for both real and imaginary roots of the equation. Follow these steps to solve a quadratic equation through this method:
- Convert the equation into the form

- Remember that while solving the equation through this method a should be equal to 1. If it is not equal to 1, then you should multiply the equation by

- Make a perfect square on the left-hand side of the equation by utilizing the value of b. You can do so by adding
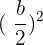 to both sides.
to both sides. - Take the square root of both sides of the equation and solve the remaining equation.
Let us now solve the following examples by completing the square method.
Example 1
Solve the equation 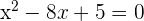 by completing the square method.
by completing the square method.
Solution
First, we will move the constant to the right hand side of the equation:
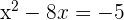
Now, we will take 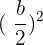 and add the resulting number on both sides of the equation.
and add the resulting number on both sides of the equation.
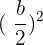
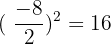

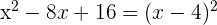
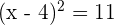
Take square root on both sides of the equation like this:
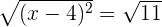
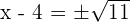
 or
or 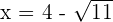
In decimal form, we can write the roots as:
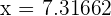 and
and 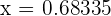
Example 2
Solve the equation 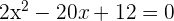 by completing the square method.
by completing the square method.
First, we will move the constant to the right hand side of the equation:
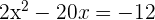
Since a should be equal to 1 to use this method, so we will divide the entire equation by 2. The new equation will be:
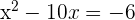
Now, we will take 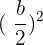 and add the resulting number on both sides of the equation.
and add the resulting number on both sides of the equation.
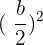
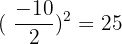


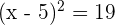
Take square root on both sides of the equation like this:
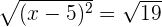
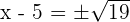
 or
or 
In decimal form, we can write the roots as:
 and
and 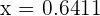
Properties of the Solutions to Quadratic Equations
Here, we will discuss some of the properties of the solutions to quadratic equations:
- The sum of the solutions of a quadratic equation is
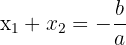
- The product of the solutions of a quadratic equation is
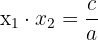
- If the roots of an equation are known, then it can be written as
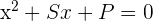 , where
, where 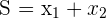 and
and 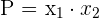
You can check for a maths tutor here.













I am impressed well done.