Chapters
Often, you might experience that applying limits results in infinity. In limits, getting infinity means something isn't right. Mathematicians dislike infinity results, but why? What is infinity and what it means in the world of limits?
What is Infinity?
Before we explain what is infinity, we want you to solve a division question, divide 
by 
(i.e.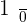 
). What quotient did you get? Is it 
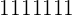or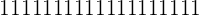 
? The problem is, we don't know! If we start writing 
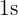from the first page of a notebook and fill the whole notebook with 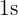still it is nothing! It will go on forever because you can't divide any number by zero. In simple words, it is undefined! And the best way to show that it will go forever, we use the infinity sign, 
. In the mathematics world, infinity means that a value that isn't defined. It is endless and we can't define that value. The best part is that we can't find this value but still we can work with it.
Infinity in Limits
Infinity can be found in every domain of maths. However, if we talk about the domain of maths that most likely will end up with infinity then limits might win. Limit means that we are testing the limit of the equation. This doesn't mean that every time we apply limits to any equation will always end in infinity. It mostly depends on the equation, for example, you have an equation,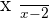 
and you applied limits at 
, what would you get? Of course, it will be infinity! But here we are testing the limits of the equation, we found that at , the equation results in infinity.
In this example, only at , the function outputs infinity but all the values other than 
and , you will get a real number. At a certain point where the function reaches infinity, our keen point would be the point before the function outputs infinity. It could be 
but there is a problem, it can still go to infinity! How many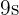 
will you add? That is why we use different methods to find the limits at infinity.
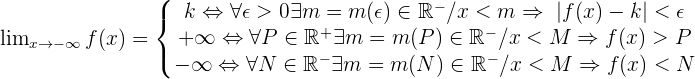
Below are more examples how you can end up with infinity in limits.
Did you like this article? Rate it!
Loading...
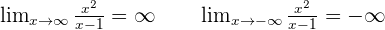
Derivative of denominator is wrong
Good catch—thanks for pointing that out! We’ll double-check the derivative in that section and make any necessary corrections. Really appreciate you taking the time to flag it. 👍
Thank you
Thank you Abbas! Good luck with your studies!
With regard to the Zero Over a Number item, is there a mis-statement? It’s immediately followed by “If a number is divided by zero which means that the numerator is zero and the denominator is the number, then the result is zero.”
Hi Mark,
You’re absolutely right to raise the question — there does appear to be a misstatement in that sentence. The phrase “If a number is divided by zero, which means that the numerator is zero and the denominator is the number…” is indeed misleading and should be corrected.
To clarify:
Zero divided by a number (e.g. 0 ÷ 5) equals 0.
A number divided by zero (e.g. 5 ÷ 0) is undefined.
We’ll update the sentence to reflect the correct mathematical explanation. We appreciate you catching that and helping us improve the accuracy of the content!
There is more than one size of infinity, though. What if you multiply the infinity of the whole numbers (Aleph-0) by the infinity of the real numbers (fraktur-c)?
Thanks a lot to you for this essentiol article.
Hi Piyash! Thanks for your comment, great to hear that you found this useful!
Very nice