Chapters

The best Maths tutors available
Exercise 1
Using the definition of a limit, prove that:
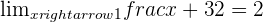
Exercise 2
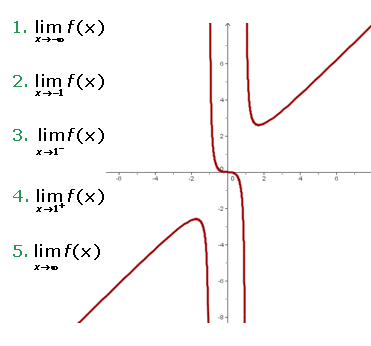
Using the graph of the function f(x), determine the following limits.
Exercise 3
Using the definition of a limit, prove that:
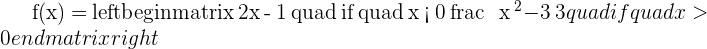 has a limit −1 as x 0
has a limit −1 as x 0
Calculate the Following Limits:
Exercise 4
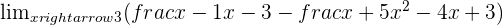
Exercise 5
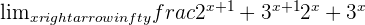
Exercise 6
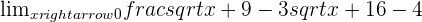
Exercise 7
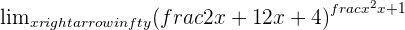
Solution of exercise 1
Using the definition of a limit, prove that:
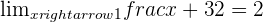
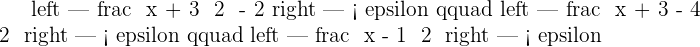

If 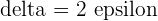
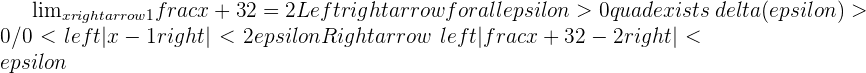
To check this, take a 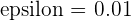 .
.
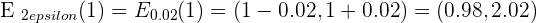
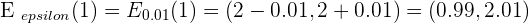
For 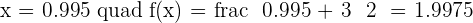 .
.
For  .
.
Solution of exercise 2
Using the graph of the function f(x), determine the following limits.
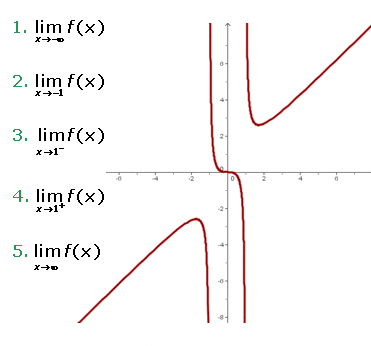
Solution of exercise 3
Using the definition of a limit, prove that:
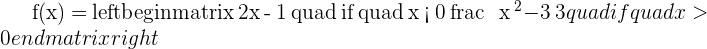 has a limit −1 as x 0
has a limit −1 as x 0
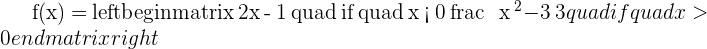
Left side limit.

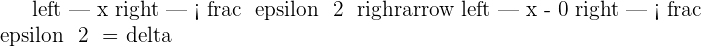


Right side limit
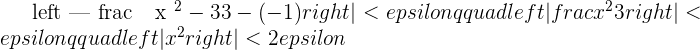


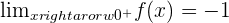
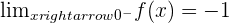
Solution of exercise 4
Calculate the limit:
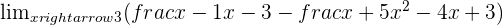

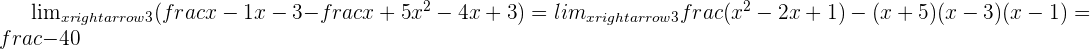
Calculate the side limits to determine the sign of  .
.

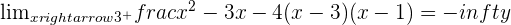
No limit.
Solution of exercise 5
Calculate the limit:
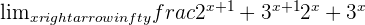
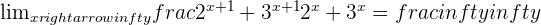

Solution of exercise 6
Calculate the limit:
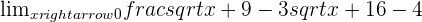




Solution of exercise 7
Calculate the limit:
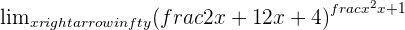
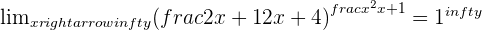
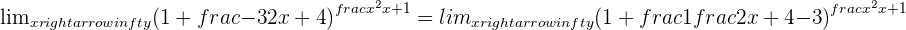
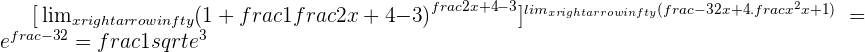
Summarise with AI:










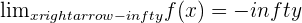
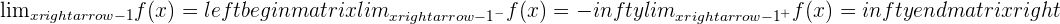
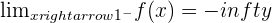
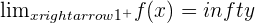




Derivative of denominator is wrong
Good catch—thanks for pointing that out! We’ll double-check the derivative in that section and make any necessary corrections. Really appreciate you taking the time to flag it. 👍
Thank you
Thank you Abbas! Good luck with your studies!
With regard to the Zero Over a Number item, is there a mis-statement? It’s immediately followed by “If a number is divided by zero which means that the numerator is zero and the denominator is the number, then the result is zero.”
Hi Mark,
You’re absolutely right to raise the question — there does appear to be a misstatement in that sentence. The phrase “If a number is divided by zero, which means that the numerator is zero and the denominator is the number…” is indeed misleading and should be corrected.
To clarify:
Zero divided by a number (e.g. 0 ÷ 5) equals 0.
A number divided by zero (e.g. 5 ÷ 0) is undefined.
We’ll update the sentence to reflect the correct mathematical explanation. We appreciate you catching that and helping us improve the accuracy of the content!
There is more than one size of infinity, though. What if you multiply the infinity of the whole numbers (Aleph-0) by the infinity of the real numbers (fraktur-c)?
Thanks a lot to you for this essentiol article.
Hi Piyash! Thanks for your comment, great to hear that you found this useful!
Very nice