Till here, you have a good concept of what is a limit and why do we use it? When you are applying a limit at a certain point, the limit is approached from the left-hand side to that value. Suppose you have a function,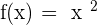 
at 
, the limit will be approached from negative infinity to the point where x is equal to 2. However, this isn't the only direction of the limit, it can be approached from infinity to the point where x is equal to 2. Both cases are correct and can be used. In this resource, you will learn the direction of limits and where it is used.
There are two types of directions of approaching and they are:
- Left-sided limit or left-hand limit,
- Right-sided limit or right-hand limit.
Normally, we use one side limit. It means that limit is approached from one direction only. It could be any either left-hand limit or right-hand limit. Both we give you the same answer but in some cases, we also use both sides. The case we are talking about is finding the continuity of the equation. To find whether the equation is continuous or not, we use both side limit and then compare it with each other. If the answers are the same, we call it continuous otherwise it is discontinuous. This is a very long topic and we will cover it in another resource, lets just stick to the limit sides.
Left-Sided Limit or Left-Hand Limit
If the direction of the approaching is from negative infinity to the point, that means it is a left-side limit. Consider the graph below:
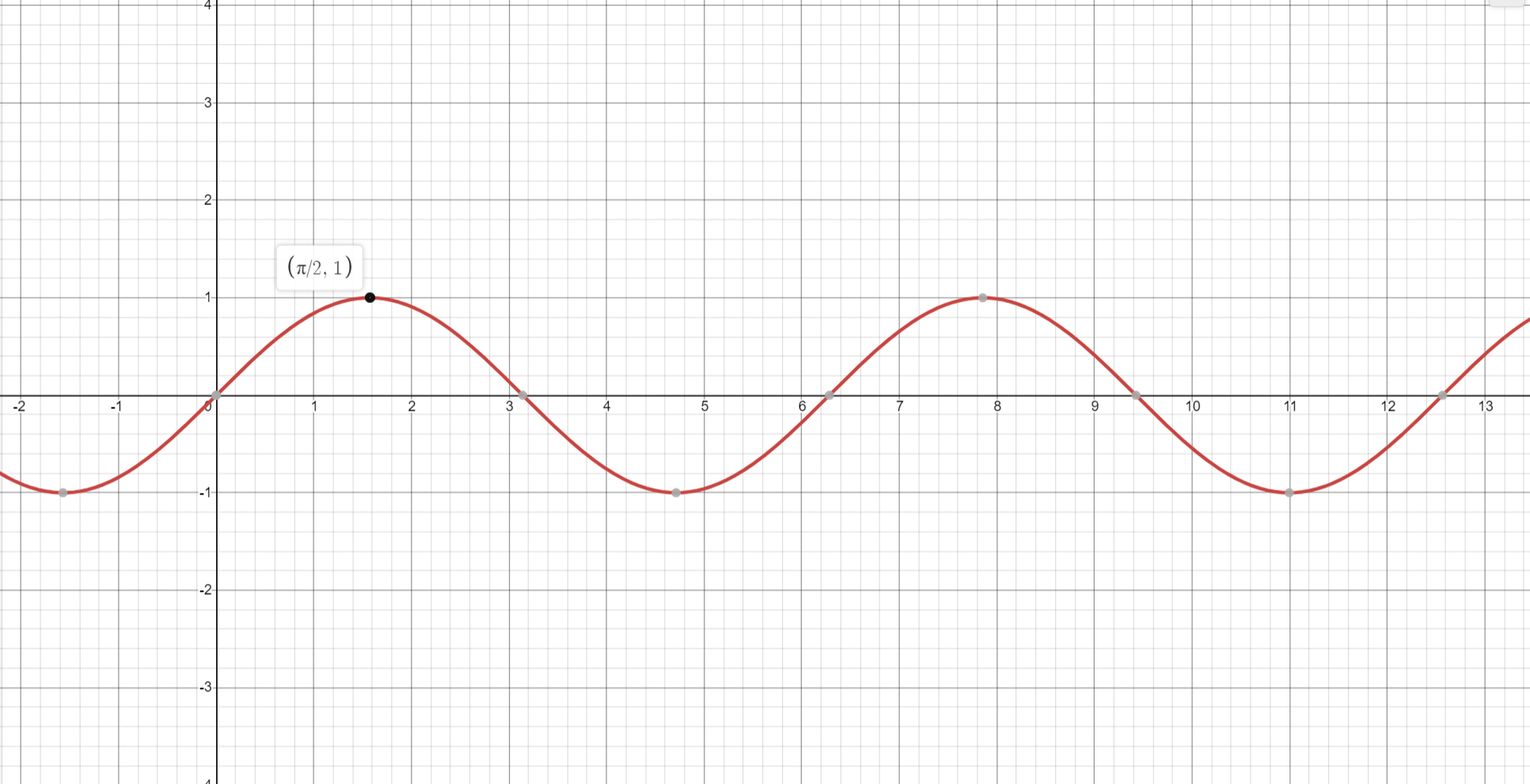
The above graph is a simple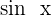 
curve. Let's say the limit is approaching the point, 
. For the case of the left-hand side limit, it will be written as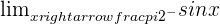 
. It means that the limit is been approached from negative infinity (which is on the left side of the graph) to the point. Hence we are travelling from the left side of the graph to the point where x is equal to 
. We call this direction the left-hand limit. Below is the syntax of the left-hand limit and its condition.
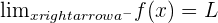
Right Sided Limit or Right Hand Limit
If the direction of the approaching is from positive infinity to the point, that means it is a right-side limit. Consider the 
graph again. Let's say this time you are approaching the point from positive infinity to . This means that you are travelling from the left side of the graph to the point where x is equal to . We call this direction the right-hand limit. Below is the syntax of the right-hand limit and its condition.
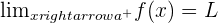
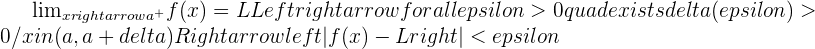
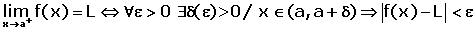
Example
The limit of a function at a point if it exists, is unique.
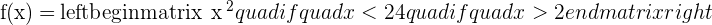
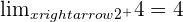
In this case, it can be seen that the limit from both the left and right-sided as x tends to 
is 
.
The limit of the function is as x tends to even though the function has no value at .
To calculate the limit of a function at a point, it is not of importance what happens at that particular point, but what happens around it.
Given the function:
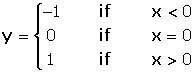
Calculate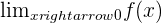 
.
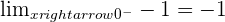
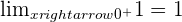
The function has no limit at 
.
Did you like this article? Rate it!
Loading...
Derivative of denominator is wrong
Good catch—thanks for pointing that out! We’ll double-check the derivative in that section and make any necessary corrections. Really appreciate you taking the time to flag it. 👍
Thank you
Thank you Abbas! Good luck with your studies!
With regard to the Zero Over a Number item, is there a mis-statement? It’s immediately followed by “If a number is divided by zero which means that the numerator is zero and the denominator is the number, then the result is zero.”
Hi Mark,
You’re absolutely right to raise the question — there does appear to be a misstatement in that sentence. The phrase “If a number is divided by zero, which means that the numerator is zero and the denominator is the number…” is indeed misleading and should be corrected.
To clarify:
Zero divided by a number (e.g. 0 ÷ 5) equals 0.
A number divided by zero (e.g. 5 ÷ 0) is undefined.
We’ll update the sentence to reflect the correct mathematical explanation. We appreciate you catching that and helping us improve the accuracy of the content!
There is more than one size of infinity, though. What if you multiply the infinity of the whole numbers (Aleph-0) by the infinity of the real numbers (fraktur-c)?
Thanks a lot to you for this essentiol article.
Hi Piyash! Thanks for your comment, great to hear that you found this useful!
Very nice