Functions come in all shapes and sizes. One of the key elements of function is either the function is continuous or not? One of the biggest examples of a non-continuous function is the piece-wise function. The graph of the function breaks at a certain limit. It means that after some inputs, the function behaves differently. You can't predict anything in a piece-wise function because it breaks at some point. On the other hand, if the function is continuous, it means that the graph will have no breaking point. The function won't behave differently on any input. The indication of a continuous function is that it will go to infinity, it will be like a graph drawn without lifting the pencil from the paper. Suppose you have a function, 
. Below is the graph of the function.
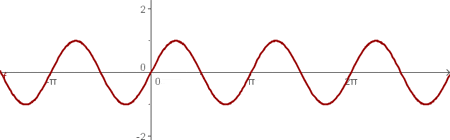
As you can see, the function keeps following a similar pattern over and over without any gap or breaking point. We will say it is a continuous function but what if someone asks you to give proof of its continuity? How to show that? Keep on reading to find it.
Continuous Function at a Point
To prove the continuity of a function, pick a point and from that point, we can prove the function's continuity. Imagine that the point you picked is 
, now a function, 
, is continuous at a point a, if and only if it meets the following conditions:
1. The point has an image. If the image of the point "a" doesn't exist, that means the point "a" doesn't belong to a continuous graph.
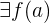
2. There is a limit of the function at . The limit approaches the point "a" from both sides, from the positive side to point "a" and from the negative side to point "a". If both sides are equal to 
that means there is no breaking in the graph.
3. The value of the function at the point coincides with the limit of the function at the point.
Example
Study the continuity of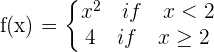 
at 
.
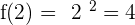
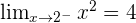
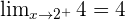
Directional Continuity
One of the conditions stated that the limit of the function approaching the point "a" should be equal to f(a),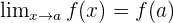 
. This means that the limit will be approached from 2 sides and if both are equal, it means the function is continuous. Those sides are "Left-continuous function" and "Right-continuous function".
Left-Continuous Function
The left-continuous function says that the limit of the function will be approached starting from left and ending to the point "a". It will go left to right and will finish at point "a".
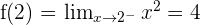
Right-Continuous Function
This time, the limit of the function will be approached from right to the point "a". This is called the right-continuous function.
Did you like this article? Rate it!
Loading...
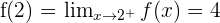
Derivative of denominator is wrong
Good catch—thanks for pointing that out! We’ll double-check the derivative in that section and make any necessary corrections. Really appreciate you taking the time to flag it. 👍
Thank you
Thank you Abbas! Good luck with your studies!
With regard to the Zero Over a Number item, is there a mis-statement? It’s immediately followed by “If a number is divided by zero which means that the numerator is zero and the denominator is the number, then the result is zero.”
Hi Mark,
You’re absolutely right to raise the question — there does appear to be a misstatement in that sentence. The phrase “If a number is divided by zero, which means that the numerator is zero and the denominator is the number…” is indeed misleading and should be corrected.
To clarify:
Zero divided by a number (e.g. 0 ÷ 5) equals 0.
A number divided by zero (e.g. 5 ÷ 0) is undefined.
We’ll update the sentence to reflect the correct mathematical explanation. We appreciate you catching that and helping us improve the accuracy of the content!
There is more than one size of infinity, though. What if you multiply the infinity of the whole numbers (Aleph-0) by the infinity of the real numbers (fraktur-c)?
Thanks a lot to you for this essentiol article.
Hi Piyash! Thanks for your comment, great to hear that you found this useful!
Very nice