In this article, we will discuss how to evaluate a given function if its limit approaches to infinity and we get an indeterminate form of infinity minus infinity. But before discussing this, first, we will see what is meant by limit of a function and l'Hôpital's Rule because both these concepts are closely related to our topic.
What is Limit?
Limit tells us how a function acts when its independent variable, i.e. x, approaches to a specific number. The formal definition of the limit concept is given below:
Consider a function (f) defined on some open interval that has a number a, except at "a" itself. We can say that the limit of f(x) as x approaches to a is L, and we can write it mathematically like this:
\lim_ {x\rightarrow a} f(x) = L
If for every number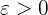 
, there is a corresponding number 
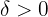in such as way that:
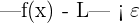
whenever:
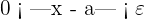
l'Hôpital's Rule
Suppose the functions f and g are differentiable, with g'(x) not zero in an interval around a, except a itself. In such a situation, one of the following points must be true:
- The limits of both the functions f(x) and g(x) are zero as x approaches a
- The functions f(x) and g(x) have infinite limit (positive or negative) as x approaches a
When one of the above discussed points are true, then the limit of the ratio of f and g, i.e.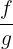 
is equal to the limit of the ratio of the differentials of the functions f ' and g ', i.e., 
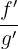{where the prime represents the appropriate derivative}, until the limit exists, or is infinite.
l'Hôpital's Rule can be applied in one of the following forms of the limit:
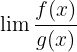, where both f(x) and g(x) approach to 0
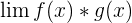, where f(x) approaches to infinity and g(x) approaches to 0
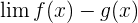, where both f(x) and g(x) approach infinity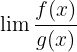- , where both f(x) and g(x) approach to infinity
, where both f(x) and g(x) approach to 0- , where f(x) approaches 1 and g(x) approaches infinity
- , where f(x) approaches to infinity and g(x) approaches to 0
In this article, we will specifically discuss how to apply the l'Hôpital's Rule when we have the indeterminate form 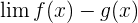, where both the functions f(x) and g(x) approach to infinity.
Example 1
Evaluate \lim_{x \rightarrow \infty} (\sqrt{x^2 - 1} - x).
Solution
The above function has an indeterminate form of 
because \lim_ {x \rightarrow \infty}(\sqrt{x^2 - 1}) is equal to 
, and \lim_ {x \rightarrow \infty} x is also equal to .
So, we will first convert the function into another indeterminate form for using the l'Hôpital's Rule. One method to convert it into another form is factoring the largest term as shown below:
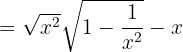
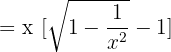
When we will apply the limit on the above function as shown below, we will still get an indeterminate form of 
.
=\lim_{x \rightarrow \infty}x [\sqrt{1 - \dfrac{1}{x^2}} - 1]
Now, we will convert the above expression into a quotient form like this:
=\lim_{x \rightarrow \infty}\frac {\sqrt{1 - \dfrac{1}{x^2}}- 1}{\dfrac{1}{x}}
Now, will apply l'Hôpital's Rule here. To apply the l'Hôpital's Rule, we will take the first derivative of numerator and denominator separately. The first derivative of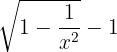 
is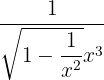 
and the derivative of 
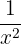is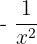 
. Now, substitute these derivatives in the function like this:
=\lim_{x \rightarrow \infty}\frac {\dfrac{1}{\sqrt{1 - \dfrac{1}{x^2}}x^3}} {- \dfrac{1}{x^2}}
Applying the limit will give us the following answer:
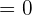
Example 2
Evaluate \lim_{x \rightarrow \infty} (\sqrt{x^2 + 5x} - x).
Solution
The above function has an indeterminate form of because \lim_ {x \rightarrow \infty}(\sqrt{x^2 + 5x}) is equal to , and \lim_ {x \rightarrow \infty} x is also equal to .
So, we will first convert the function into another indeterminate form in order to use the l'Hôpital's Rule. One method to convert it into another form is factoring the largest term as shown below:
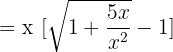
When we will apply the limit on the above function as shown below, we will still get an indeterminate form:
=\lim_{x \rightarrow \infty}x [\sqrt{1 + \dfrac{5x}{x^2}} - 1]
Now, we will convert the above expression into a quotient form like this:
=\lim_{x \rightarrow \infty}\frac {\sqrt{1 + \dfrac{5x}{x^2}} - 1}{\dfrac{1}{x}}
Now, will apply l'Hôpital's Rule here. To apply the l'Hôpital's Rule, we will take the first derivative of numerator and denominator separately. The first derivative of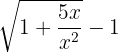 
is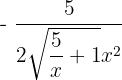 
and the derivative of 
is 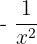. Now, substitute these derivatives in the function like this:
=\lim_{x \rightarrow \infty} -\frac {\frac{5}{2\sqrt{\frac{5}{x} +1} x^2}} {\dfrac{1}{x^2}}
Applying the limit (x approaches to infinity) will give us the following answer:
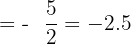
We can also use conjugate to evaluate such indeterminate function. In the next two examples, we will use the conjugate method to evaluate the given functions.
Example 3
Evaluate \lim_{x \rightarrow \infty} (\sqrt{x^2 + 3x} - x).
Solution
The above function has an indeterminate form of because \lim_ {x \rightarrow \infty} (\sqrt{x^2 + 3x} is equal to , and \lim_ {x \rightarrow \infty} x is also equal to .
We will use the conjugate of the function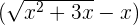 
to evaluate the function. The conjugate of 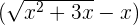is 
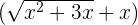. Multiply and divide the original function by this conjugate as shown below:
=\lim_{x \rightarrow \infty} (\sqrt{x^2 + 3x} - x) \cdot \frac {\sqrt{x^2 + 3x} + x} {\sqrt{x^2 + 3x} + x}
=\lim_{x \rightarrow \infty} (\sqrt{x^2 + 3x} - x) \cdot \frac {\sqrt{x^2 + 3x} + x} {\sqrt{x^2 + 3x} + x}
=\lim_{x \rightarrow \infty} \frac{(\sqrt{x^2 + 3x} - x)^2} {\sqrt{x^2 + 3x} + x}
=\lim_{x \rightarrow \infty} \frac{3x} {\sqrt{x^2 + 3x} + x}
Now, we will factor out the biggest term in the denominator and write the expression like this:
=\lim_{x \rightarrow \infty} \frac{3x} {\sqrt {x^2} (\sqrt{1 + \frac{3x}{x^2}} + x}
=\lim_{x \rightarrow \infty} \frac{3x} {x (\sqrt{1 + \frac{3x}{x^2}} + 1)}
=\lim_{x \rightarrow \infty} \frac{3x} {x (\sqrt{1 + \frac{3x}{x^2}} + 1)}
=\lim_{x \rightarrow \infty} \frac{3} { (\sqrt{1 + \frac{3}{x}} + 1)}
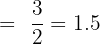
Example 4
Evaluate \lim_{x \rightarrow \infty} (\sqrt{x^2 + x} - x).
Solution
The above function has an indeterminate form of because \lim_ {x \rightarrow \infty} (\sqrt{x^2 + x} is equal to , and \lim_ {x \rightarrow \infty} x is also equal to .
We will use the conjugate of the function 
to evaluate it. The conjugate of is 
. Multiply and divide the original function by this conjugate as shown below:
=\lim_{x \rightarrow \infty} (\sqrt{x^2 + x} - x) \cdot \frac {\sqrt{x^2 + x} + x} {\sqrt{x^2 + x} + x}
=\lim_{x \rightarrow \infty} \frac{(\sqrt{x^2 + x} - x)^2} {\sqrt{x^2 + x} + x}
=\lim_{x \rightarrow \infty} \frac{x} {\sqrt{x^2 + x} + x}
Now, we will factor out the biggest term in the denominator and write the expression like this:
=\lim_{x \rightarrow \infty} \frac{x} {\sqrt {x^2} (\sqrt{1 + \frac{x}{x^2}} + x}
=\lim_{x \rightarrow \infty} \frac{x} {x (\sqrt{1 + \frac{x}{x^2}} + 1)}
=\lim_{x \rightarrow \infty} \frac{1} { (\sqrt{1 + \dfrac{1}{x}} + 1)}
Did you like this article? Rate it!
Loading...
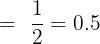
Derivative of denominator is wrong
Good catch—thanks for pointing that out! We’ll double-check the derivative in that section and make any necessary corrections. Really appreciate you taking the time to flag it. 👍
Thank you
Thank you Abbas! Good luck with your studies!
With regard to the Zero Over a Number item, is there a mis-statement? It’s immediately followed by “If a number is divided by zero which means that the numerator is zero and the denominator is the number, then the result is zero.”
Hi Mark,
You’re absolutely right to raise the question — there does appear to be a misstatement in that sentence. The phrase “If a number is divided by zero, which means that the numerator is zero and the denominator is the number…” is indeed misleading and should be corrected.
To clarify:
Zero divided by a number (e.g. 0 ÷ 5) equals 0.
A number divided by zero (e.g. 5 ÷ 0) is undefined.
We’ll update the sentence to reflect the correct mathematical explanation. We appreciate you catching that and helping us improve the accuracy of the content!
There is more than one size of infinity, though. What if you multiply the infinity of the whole numbers (Aleph-0) by the infinity of the real numbers (fraktur-c)?
Thanks a lot to you for this essentiol article.
Hi Piyash! Thanks for your comment, great to hear that you found this useful!
Very nice