Whether the function is continuous or not is also important data. Functions can be distinguished on the basis of continuity. Polynomial, rational, radical, exponential, logarithmic and trigonometric functions are continuous at all points of their domain. So, what is a continuous function? Keep on reading to find out.

Continuous Function
Take a pencil and graph paper and draw a line. Start from one end and finish it to the opposite end without lifting the pencil. You will see a proper line without any breaks in between. We will call the function continuous. There is only one condition for a continuous function and that is there should be not a single breakpoint. It should be like a graph drawn without lifting the pencil from the graph. If there is some kind of breakpoint, it won't be a continuous function.
Of course, that line will have an equation. Let's say the equation is  . Below is the graph of
. Below is the graph of  .
.
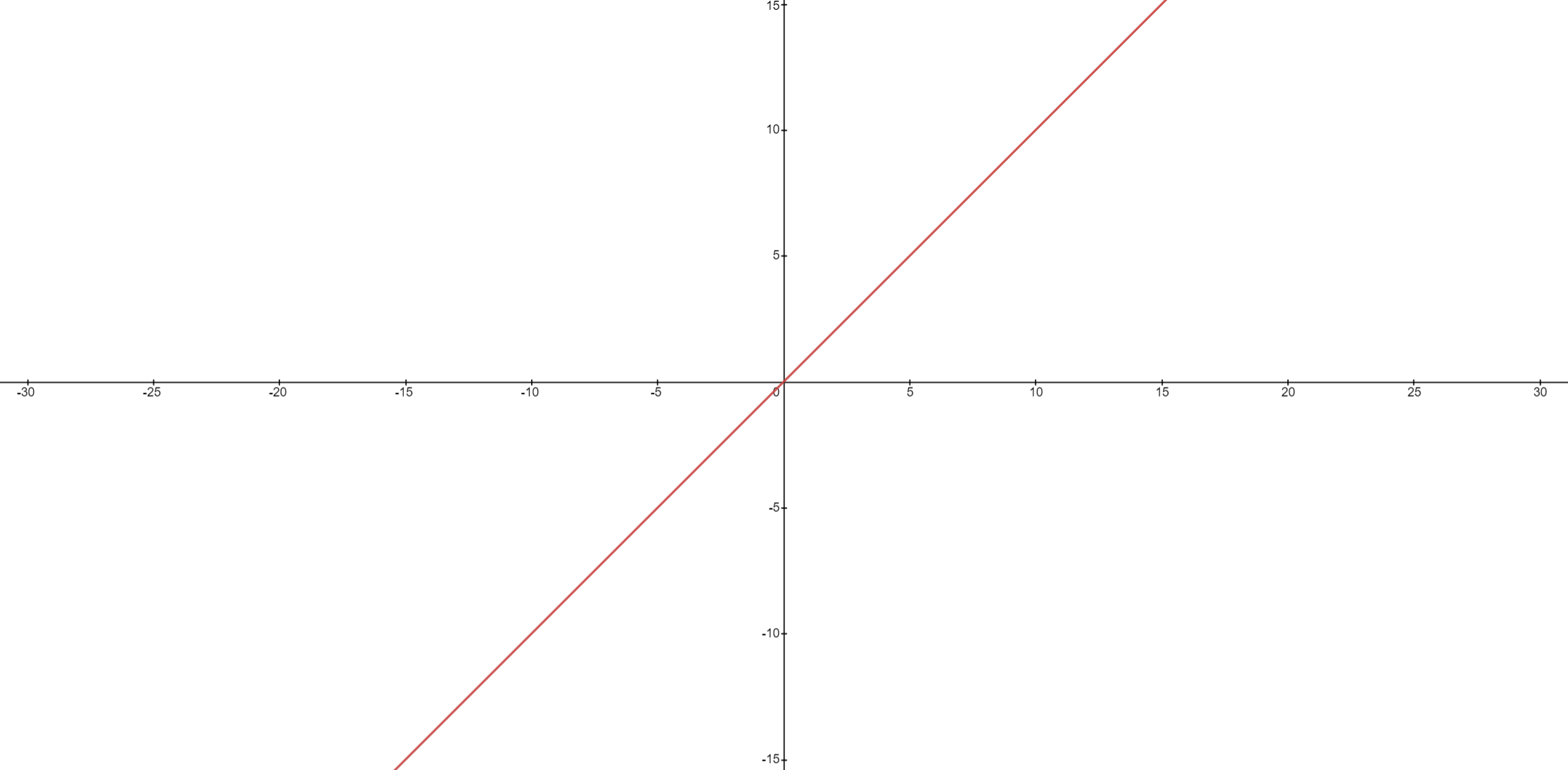
Let's gather some data, we know at when x is equal to 15, y will also be equal to 15. When x is equal to 2, y is also equal to 2. The graph is plotted from 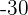 to
to 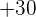 for abscissa and
for abscissa and  to
to 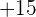 for ordinate. However, you want to find what will be the value of y when x is equal to
for ordinate. However, you want to find what will be the value of y when x is equal to 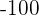 ? Do you need to draw the graph again? No, you can predict the value, the value of y will be
? Do you need to draw the graph again? No, you can predict the value, the value of y will be 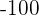 because the function is continuous. This example shows that we can make predictions of higher values if the function is continuous. What if there is a breakpoint in the graph?
because the function is continuous. This example shows that we can make predictions of higher values if the function is continuous. What if there is a breakpoint in the graph?
Discontinuity
Suppose you have a function,  . Let's plot it on the graph.
. Let's plot it on the graph.
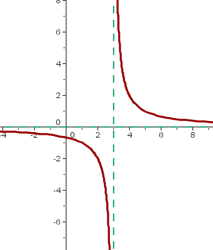
At  , we see that the function is going to infinity from both sides. It seems that the pencil is lifted up to draw the second curve. Both lines don't meet each other and there is a gap between them. We call them discontinuous function. There are many types of discontinuous functions, they are:
, we see that the function is going to infinity from both sides. It seems that the pencil is lifted up to draw the second curve. Both lines don't meet each other and there is a gap between them. We call them discontinuous function. There are many types of discontinuous functions, they are:
- Jump discontinuity
- Point discontinuity
- Infinite discontinuity
These types of discontinuous are in detail and deserve their own resource which we will talk about later. In the case of the graph, the function  is continuous at
is continuous at 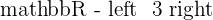 . At
. At  it is not continuous because the function does not exist at this point.
it is not continuous because the function does not exist at this point.
Piecewise Functions
In the above example, we talked about a single equation that is defined by a function, i.e.  . Normally, a function doesn't have a single equation, it might be defined by multiple equations within a single function with their ranges. We call them piecewise function. Piecewise functions are continuous if every function is in its interval of definition, and if the functions match their side limits at the points of separation of their intervals. For example, we have a function,
. Normally, a function doesn't have a single equation, it might be defined by multiple equations within a single function with their ranges. We call them piecewise function. Piecewise functions are continuous if every function is in its interval of definition, and if the functions match their side limits at the points of separation of their intervals. For example, we have a function, 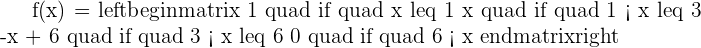 . Let's plot it and check what comes up.
. Let's plot it and check what comes up.

Although there are multiple equations within a function, however, their ranges are coinciding in a way that the pencil was not lifted while plotting this graph. In conclusion, the function 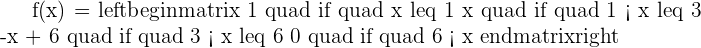 is continuous at
is continuous at  , because its constituent functions are polynomial and the side limits at the points of division coincide. Please do note that not all piecewise functions are continuous. They can be continuous and they can be discontinuous. Since we are talking about continuity, we made this example to show how piecewise function can be continuous.
, because its constituent functions are polynomial and the side limits at the points of division coincide. Please do note that not all piecewise functions are continuous. They can be continuous and they can be discontinuous. Since we are talking about continuity, we made this example to show how piecewise function can be continuous.
In Nutshell
If f and g are continuous at  , then:
, then:
 is continuous at
is continuous at  .
.
 is continuous at
is continuous at  .
.
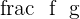 is continuous at
is continuous at  , if
, if 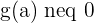 .
.
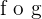 is continuous at
is continuous at  .
.
Summarise with AI:













Derivative of denominator is wrong
Good catch—thanks for pointing that out! We’ll double-check the derivative in that section and make any necessary corrections. Really appreciate you taking the time to flag it. 👍
Thank you
Thank you Abbas! Good luck with your studies!
With regard to the Zero Over a Number item, is there a mis-statement? It’s immediately followed by “If a number is divided by zero which means that the numerator is zero and the denominator is the number, then the result is zero.”
Hi Mark,
You’re absolutely right to raise the question — there does appear to be a misstatement in that sentence. The phrase “If a number is divided by zero, which means that the numerator is zero and the denominator is the number…” is indeed misleading and should be corrected.
To clarify:
Zero divided by a number (e.g. 0 ÷ 5) equals 0.
A number divided by zero (e.g. 5 ÷ 0) is undefined.
We’ll update the sentence to reflect the correct mathematical explanation. We appreciate you catching that and helping us improve the accuracy of the content!
There is more than one size of infinity, though. What if you multiply the infinity of the whole numbers (Aleph-0) by the infinity of the real numbers (fraktur-c)?
Thanks a lot to you for this essentiol article.
Hi Piyash! Thanks for your comment, great to hear that you found this useful!
Very nice