Chapters
The mathematical equation 
\lim_{x \rightarrow a} f (x) = \infty states that whenever x is closer to but not equal to a, then the function f(x) is a large positive number. A limit having a value of infinity means that when x approaches to a, the function f(x) becomes bigger and bigger. It means that the function increases without any limit or boundary.
Similarly, the mathematical equation \lim_{x \rightarrow a} f (x) = \infty states that as x approaches to a, the function f(x) is a large positive number, and as x approaches to a, the value of the function f(x) decreases without limit.
Whenever we say that lim = 
, it means that the limit does not exist. The limit \lim _ {x \rightarrow a} f(x) = L exists only if L is a number. Infinity is not a number as it simply means that something exists without a boundary. If the limit is positive, then it means that the function increases without any limit. If the limit is negative, then it simply means that the function decreases without any limit.
Definition of Infinite Limits
In this section, we will define three types of infinite limits.
a) Infinite limits from the left
Suppose f(x) is a function that is defined at all the values in an open interval of the form (b, a)
- If the values of the function f(x) increase without limit as the values of x (where x is less than a) get closer to the number a, then we can say that the limit as x gets closer to a, from the left is positive infinity and we can write it as:
\lim _ {x \rightarrow a ^{-}} f(x) = + \infty
- If the values of the function f(x) decrease without limit as the values of x (where x is less than a) get closer to the number a, then we can say that the limit as x gets closer to a, from the left is negative infinity and we can write it as:
\lim _ {x \rightarrow a ^{-}} f(x) = - \infty
b) Infinite limits from the right
- If the values of the function f(x) increase without limit as the values of x (where x is greater than a) get closer to the number a, then we can say that the limit as x gets closer to a, from the left is positive infinity and we can write it as:
\lim _ {x \rightarrow a ^{+}} f(x) = + \infty
- If the values of the function f(x) decrease without limit as the values of x (where x is greater than a) get closer to the number a, then we can say that the limit as x gets closer to a, from the left is negative infinity and we can write it as:
\lim _ {x \rightarrow a ^{+}} f(x) = - \inftylimx→a−f(x)=+∞.(2.4.2)(2.4.2)limx→a−f(x)=+∞.
c) Two sided infinite limits
Suppose the function f(x) is defined for all 
in an open interval that contains a. Then,
- If the values of the function f(x) increase without limit as the values of x (where x is not equal to a), get closer to the number a, then we can say that the limit as x becomes closer to the number a is positive infinity. We can mathematically write it as:
\lim _ {x \rightarrow a} f (x) = + \infty
- If the values of the function f(x) decrease without any limit as the values of x (where x is not equal to a) get closer to the number a, then we can say that the limit as x gets closer to the number a is negative infinity. We can write it mathematically like this:
\lim _ {x \rightarrow a} f (x) = - \infty
It is important to consider a point that when we say that \lim_{x \rightarrow a} f(x) = + \infty or \lim_{x \rightarrow a} f(x) = - \infty, then we are telling the behavior of the function. We are not telling through these notations that the limit exists.
Examples
Evaluate the following limits:
1) \lim _ {x \rightarrow {0 ^{-}}} \frac{1}{2x}
The values of the function 
decrease without limit as x becomes closer to 0 from the left. Hence, we can conclude that:
\lim _ {x \rightarrow {0 ^{-}}} \frac{1}{2x}= - \infty
2) \lim _ {x \rightarrow {0 ^{+}}} \frac{1}{2x}
The values of the function increase without limit as x becomes closer to 0 from the right. Hence, we can conclude that:
\lim _ {x \rightarrow {0 ^{+}}} \frac{1}{2x}= + \infty
3) Evaluate \lim_{x \rightarrow 4 ^ {-}} \frac {8} {(x - 4)^3}
We know that if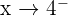 
, then we are acknowledging the fact that the value of x is less than 4. Hence, we can say that:
\lim_{x \rightarrow 4 ^ {-}} \frac {8} {(x - 4)^3} = - \infty
4) Evaluate \lim_{x \rightarrow 4 ^ {+}} \frac {8} {(x - 4)^3}
We know that if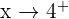 
, then we are acknowledging the fact that the value of x is greater than 4. Hence, we can say that:
\lim_{x \rightarrow 4 ^ {+}} \frac {8} {(x - 4)^3} = + \infty
Did you like this article? Rate it!
Loading...
Thank you
Thank you Abbas! Good luck with your studies!
With regard to the Zero Over a Number item, is there a mis-statement? It’s immediately followed by “If a number is divided by zero which means that the numerator is zero and the denominator is the number, then the result is zero.”
Hi Mark,
You’re absolutely right to raise the question — there does appear to be a misstatement in that sentence. The phrase “If a number is divided by zero, which means that the numerator is zero and the denominator is the number…” is indeed misleading and should be corrected.
To clarify:
Zero divided by a number (e.g. 0 ÷ 5) equals 0.
A number divided by zero (e.g. 5 ÷ 0) is undefined.
We’ll update the sentence to reflect the correct mathematical explanation. We appreciate you catching that and helping us improve the accuracy of the content!
There is more than one size of infinity, though. What if you multiply the infinity of the whole numbers (Aleph-0) by the infinity of the real numbers (fraktur-c)?
Thanks a lot to you for this essentiol article.
Hi Piyash! Thanks for your comment, great to hear that you found this useful!
Very nice
🚇🌋⚓️🛳️✈️🛸🚅🛬🚆♟️