Chapters
Discontinuity means that there is a breakpoint in the graph. For example, you are drawing a sinusoidal graph, at a point, you lift up the pencil. That point is the breaking point of the graph. It means that the graph will break its continuity at that point. Hence, we will call it a discontinuous function. There are three conditions for continuity. If any of the following three continuity conditions are not met, the function is discontinuous at  . Here is an example of a discontinuous function.
. Here is an example of a discontinuous function.
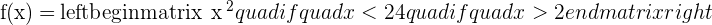
The function is discontinuous at  because there is no image.
because there is no image.

Types of Discontinuous Functions
Of course, there are different types of discontinuous function. It means that there are different ways that will make a function discontinuous. Below are the types of discontinuous functions:
Jump Discontinuity
Jump discontinuity or step discontinuity is a type of discontinuity that occurs at a point at which the line or curve breaks and changes its behaviour. For example,
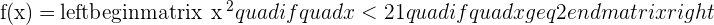

The function is discontinuous at  because there is no limit.
because there is no limit.
Point/Removable Discontinuity
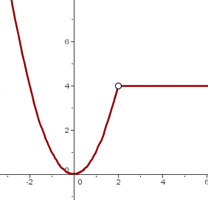
Removable discontinuity is another type of discontinuous function. It happens when a point/points from the graph behaves differently. For example,


The function is almost continuous except at the point  . The function has a different behaviour at this point which we can say that it is an anomaly. These anomalies cause discontinuity and we call them removable discontinuity. In conclusion, the function is discontinuous at x = 2 because the image does not match the limit.
. The function has a different behaviour at this point which we can say that it is an anomaly. These anomalies cause discontinuity and we call them removable discontinuity. In conclusion, the function is discontinuous at x = 2 because the image does not match the limit.
Essential Discontinuity
Last but not least, Essential discontinuity is like any other discontinuity but it doesn't occur on a point, it has an asymptote that makes the function discontinuous. For example,
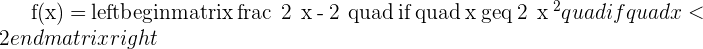 .
.

At  there is an essential discontinuity because the right-side limit is infinite. Draw a line on
there is an essential discontinuity because the right-side limit is infinite. Draw a line on  , it becomes an asymptote. Other types of discontinuous function occur on point but in the case of essential discontinuity, it has an asymptote that breaks the function.
, it becomes an asymptote. Other types of discontinuous function occur on point but in the case of essential discontinuity, it has an asymptote that breaks the function.













Derivative of denominator is wrong
Good catch—thanks for pointing that out! We’ll double-check the derivative in that section and make any necessary corrections. Really appreciate you taking the time to flag it. 👍
Thank you
Thank you Abbas! Good luck with your studies!
With regard to the Zero Over a Number item, is there a mis-statement? It’s immediately followed by “If a number is divided by zero which means that the numerator is zero and the denominator is the number, then the result is zero.”
Hi Mark,
You’re absolutely right to raise the question — there does appear to be a misstatement in that sentence. The phrase “If a number is divided by zero, which means that the numerator is zero and the denominator is the number…” is indeed misleading and should be corrected.
To clarify:
Zero divided by a number (e.g. 0 ÷ 5) equals 0.
A number divided by zero (e.g. 5 ÷ 0) is undefined.
We’ll update the sentence to reflect the correct mathematical explanation. We appreciate you catching that and helping us improve the accuracy of the content!
There is more than one size of infinity, though. What if you multiply the infinity of the whole numbers (Aleph-0) by the infinity of the real numbers (fraktur-c)?
Thanks a lot to you for this essentiol article.
Hi Piyash! Thanks for your comment, great to hear that you found this useful!
Very nice