Chapters
When we first learn exponents, it seems straightforward:
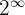should be infinitely large.
should be zero.- And since
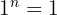, for all finite n, maybe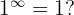 
Surprisingly, 
is not well-defined. In calculus, it’s called an indeterminate form. That means its value depends on the situation.
Understanding why requires tools from limits and sometimes L’Hôpital’s Rule. Let’s break it down.
Why is One to the Power of Infinity Indeterminate?
Infinity is not a number—it’s a concept. When you see something like , it usually comes from a limit where the base is approaching 1 while the exponent is growing without bound.
Example:
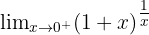
Here, the base (1 + x) approaches 1, while the exponent 1/x grows infinitely. That’s what creates the indeterminate form .
Indeterminate Forms Recap
In calculus, some expressions don’t immediately give clear answers. They’re called indeterminate forms, such as:
| Operation | Rule / Result | Notes |
|---|---|---|
| ∞ - ∞ | Indeterminate | Cannot be determined. |
| ∞ × 0 | Indeterminate | Undefined result. |
| ∞ ÷ ∞ | Indeterminate | Depends on context (limits). |
| 0^0 | Indeterminate | Sometimes treated as 1, sometimes undefined. |
| ∞^0 | Indeterminate | No fixed result. |
| 1^∞ | Indeterminate | Depends on the limit process. |
These require careful analysis with limits to find their true value.
L’Hôpital’s Rule is one of the most powerful tools for resolving indeterminate forms.
It states:
If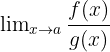
gives 
or 
, then: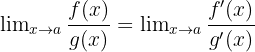
provided the limit on the right exists.
How to Handle One to the Power of Infinity
Suppose:
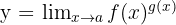
gives .
Steps:
Take the natural logarithm:
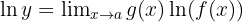
Simplify the limit:
If it becomes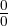 
or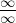 
, apply L’Hôpital’s Rule.
Solve for ln(y)
Exponentiate to return to y
Example
Evaluate:
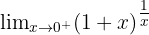
Step 1: Let
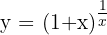
Take natural logs:
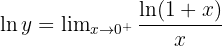
Step 2: Both numerator and denominator →0. Apply L’Hôpital’s Rule:
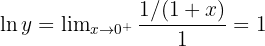
Step 3: Exponentiate to solve for y:
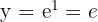
Practice Questions & Solutions
Evaluate:
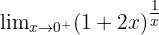
Let
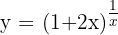
Take natural logs:
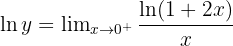
Apply L’Hôpital’s Rule:
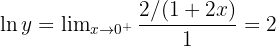
Exponentiate:
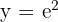
Evaluate:
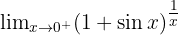
Let
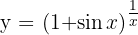
Take natural logs:
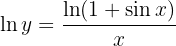
As :
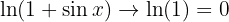
Denominator:
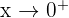
So the form is 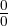, perfect for L’Hôpital’s Rule.
Differentiate numerator and denominator (using the chain rule):
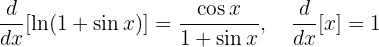
Therefore:
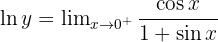
At x=0:
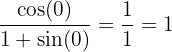
So:
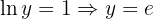
Evaluate:
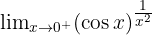
Let
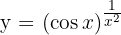
Take natural logs:
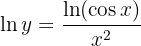
For small x, use the expansion:
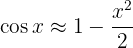
Thus,
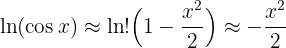
So,
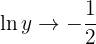
Exponentiate:
Did you like this article? Rate it!
Loading...
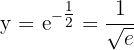
Derivative of denominator is wrong
Good catch—thanks for pointing that out! We’ll double-check the derivative in that section and make any necessary corrections. Really appreciate you taking the time to flag it. 👍
Thank you
Thank you Abbas! Good luck with your studies!
With regard to the Zero Over a Number item, is there a mis-statement? It’s immediately followed by “If a number is divided by zero which means that the numerator is zero and the denominator is the number, then the result is zero.”
Hi Mark,
You’re absolutely right to raise the question — there does appear to be a misstatement in that sentence. The phrase “If a number is divided by zero, which means that the numerator is zero and the denominator is the number…” is indeed misleading and should be corrected.
To clarify:
Zero divided by a number (e.g. 0 ÷ 5) equals 0.
A number divided by zero (e.g. 5 ÷ 0) is undefined.
We’ll update the sentence to reflect the correct mathematical explanation. We appreciate you catching that and helping us improve the accuracy of the content!
There is more than one size of infinity, though. What if you multiply the infinity of the whole numbers (Aleph-0) by the infinity of the real numbers (fraktur-c)?
Thanks a lot to you for this essentiol article.
Hi Piyash! Thanks for your comment, great to hear that you found this useful!
Very nice