Chapters
Limit is an important concept of calculus that specifies the value the function approaches as the input of the function gets closer and closer to a specific number. This concept is the foundation of calculus. In this article, we will discuss the limit rules or laws of the limit with examples. But before proceeding to these rules, first, we will discuss the concept of limit in detail.
Limit - Introduction
The limit in mathematics is defined as a value that is approached by the function's output for the given values of input. The concept of limit is very important in mathematics and calculus as it helps to define integrals, continuity and derivatives. This concept is also used to analyze a process because it tells us the behavior of the function at a specific point. Integration is an important concept of calculus. We all know that there are two types of integrals known as definite integrals and indefinite integrals. The definite integrals have upper and lower limits that are defined properly. On the other hand, upper and lower limits do not exist in indefinite integrals.
In the next section, you will find the formal definition of the limit along with the mathematical notation.
Limit - Definition
Limits tell us how a function performs when its independent variable, i.e., x, approaches a specific value. The proper definition of limit is given below:
Consider a function f that is defined on a specific open interval that has a number "a", except at "a" itself. Thus, we can say that the limit of f(x) as x approaches to "a" is L. The mathematical notation of this statement is given below:
\lim_ {x\rightarrow a} f(x) = L
Consider that for every number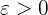 
, there is a corresponding number 
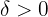in such as way that:
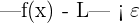
whenever:
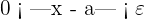
Now, we will discuss some of the rules of limit along with the relevant examples.
Limit Sum Rule
The limit sum rule states that the limit of the sum is equal to the sum of the limits. Mathematically, we can write this rule as:
\lim_{x \rightarrow a} [f(x) + g(x)] = \lim_{x \rightarrow a} f(x) + \lim_{x \rightarrow a} g(x)
Example
Evaluate the function \lim_{x \rightarrow 2} 2x^2 + 3x
Solution
We will use the limit sum rule here as there is a positive sign between the two terms of the function.
= \lim_{x \rightarrow 2} 2x ^2 + \lim_{x \rightarrow 2} 3x
Limit Difference Rule
The limit difference rule states that the limit of the difference is equal to the difference of the limits. Mathematically, we can write this rule as:
\lim_{x \rightarrow a} [f(x) - g(x)] = \lim_{x \rightarrow a} f(x) - \lim_{x \rightarrow a} g(x)
Example
Evaluate the function \lim_{x \rightarrow -1} 5x^2 - 7x
Solution
We will use the limit difference rule here as there is a negative sign between the two terms of the function.
= \lim_{x \rightarrow -1} 5x ^2 - \lim_{x \rightarrow -1} 7x
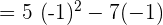
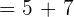
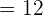
Limit Constant Rule
This rule states that the limit of the constant function is equal to the constant. Mathematically, we can write it as:
\lim_{x \rightarrow a} k = k
Example
Evaluate the function \lim_{x \rightarrow a} 12.
Solution
The limit of the constant is equal to the constant itself. So, the limit of this function is equal to 12.
Constant Multiple Rule
This rule states that the limit of constant multiplied by the function is equal to the product of constant and the limit of the function. Mathematically, we can write this rule like this:
\lim_{x \rightarrow a} c f(x) = c \lim_{x \rightarrow a}f(x)
Example
Evaluate the limit \lim_{x \rightarrow -1} 3 (x^3 + x^2 + x)
Solution
Here, we will first take limit of the function and then multiply the obtained value with constant term. We will find the limit of the function using limit sum rule because there is a positive sign between three terms.
=3 \cdot \lim_{x \rightarrow -1} x^3 + \lim_{x \rightarrow -1} x^2 + \lim_{x \rightarrow -1} x
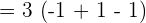
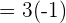
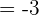
Limit Product Rule
This rule says that the limit of the product of two functions is equal to the product of the limits of two functions. Mathematically, we can write this rule as:
\lim_{x \rightarrow a} [ f(x) g (x)] = \lim_{x \rightarrow a} f(x) \cdot \lim_{x \rightarrow a} g(x)
Example
Evaluate the function \lim_{x \rightarrow 2} 4x sin x^3.
Solution
In this example, we will employ the limit product rule because two separate functions are multiplied with each other. The first function is 4x and the second one is 
.
=\lim_{x \rightarrow 2} 4x \cdot \lim_{x \rightarrow 10} sin x^3
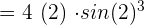
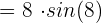
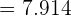
Limit Quotient Rule
This rule states that the limit of the quotient is equal to the quotient of the limits. Mathematically, we can denote this rule like this:
\lim_ {x \rightarrow a} \frac {f (x) } {g(x)} = \frac{\lim_ {x \rightarrow a} f(x)} {\lim_ {x \rightarrow a} g(x)}}
Example
Evaluate the function \lim_ {x \rightarrow 2} \frac {6x + 5}{x^2 + 3x}
Solution
We will use the limit quotient rule here. To use this rule, first, we will apply the limits separately to the numerator and the denominator and then take the quotient.
= \frac{\lim_ {x \rightarrow 2} 6x + 5} {\lim_ {x \rightarrow 2} x^2 + 3x}}
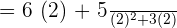
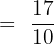
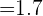
Limit Power Rule
This rule states that the limit of the function involving a power is equal to the limit of the function raised to the power. Mathematically, we can denote this rule as shown below:
\lim_ {x \rightarrow a} [f(x)]^n = [\lim_ {x \rightarrow a} f(x)]^n
Example
Evaluate the function \lim_ {x \rightarrow 1} [x^2 + 8x]^2.
Solution
Here, we will use the limit power rule.
=[\lim_ {x \rightarrow 1} x^2 + 8x]^2
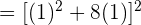
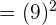
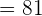
Limit of a Square Root Function
This rule states that the limit of the square root function is equal to the square root of the limit of the radicand. The same rule applies for the higher roots. Mathematically, we denote this rule like this:
\lim_ {x \rightarrow a} \sqrt {f(x)} = \sqrt { \lim_ {x \rightarrow a} f(x)}
Example 1
Evaluate the function \lim_ {x \rightarrow 2} \sqrt {3x^2 + 9x}.
Solution
We can write this function as:
= \sqrt { \lim_ {x \rightarrow 2} 3x^2 + 9x}
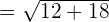
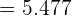
Example 2
Evaluate the function \lim_ {x \rightarrow 3} \sqrt [3] {9x^2 + x}.
Solution
We can write this function as:
= \sqrt [3] { \lim_ {x \rightarrow 2} 9x^2 + x}
Did you like this article? Rate it!
Loading...
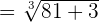
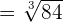
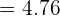
Derivative of denominator is wrong
Good catch—thanks for pointing that out! We’ll double-check the derivative in that section and make any necessary corrections. Really appreciate you taking the time to flag it. 👍
Thank you
Thank you Abbas! Good luck with your studies!
With regard to the Zero Over a Number item, is there a mis-statement? It’s immediately followed by “If a number is divided by zero which means that the numerator is zero and the denominator is the number, then the result is zero.”
Hi Mark,
You’re absolutely right to raise the question — there does appear to be a misstatement in that sentence. The phrase “If a number is divided by zero, which means that the numerator is zero and the denominator is the number…” is indeed misleading and should be corrected.
To clarify:
Zero divided by a number (e.g. 0 ÷ 5) equals 0.
A number divided by zero (e.g. 5 ÷ 0) is undefined.
We’ll update the sentence to reflect the correct mathematical explanation. We appreciate you catching that and helping us improve the accuracy of the content!
There is more than one size of infinity, though. What if you multiply the infinity of the whole numbers (Aleph-0) by the infinity of the real numbers (fraktur-c)?
Thanks a lot to you for this essentiol article.
Hi Piyash! Thanks for your comment, great to hear that you found this useful!
Very nice