Chapters
Why Division by Zero is Undefined in Arithmetic
In standard arithmetic, the operation of division by zero is undefined. It does not equal infinity or any other number.
The reason for this lies in the definition of division. Division is the inverse (opposite) of multiplication.
For example, we know that 10 divided by 2 = 5.
This statement is true because the inverse is true: 2 x 5 = 10.
Now, let's try to divide 10 by 0. Let's assume the answer is some number, x:
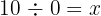
For this to be true, the inverse multiplication must also be true:
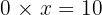
This is impossible. Any number multiplied by 0 is always 0, it can never be 10. Because no number x can solve this equation, the operation 10 divided by 0 is undefined.
What about 0 divided 0?
This is also undefined, but for a different reason. If 0 divided 0 = x, then 0 times x = 0.
The problem here is that every number works; x could be 1, 5, or -100. Since there isn't one unique answer, this is called an indeterminate form and is also not a defined number.
From 'Undefined' to 'Infinity': The Limit Concept
So, if division by zero is undefined, why do we talk about "infinity"(
) in calculus?
In calculus, we are often not actually dividing by zero. Instead, we are finding the limit of a function as it approaches a value that makes the denominator zero. This usually happens at a vertical asymptote (a line that seems to coincide with the function but doesn't quite meet it.
When we have a limit where the numerator approaches a non-zero constant (let's call it k) and the denominator approaches zero, the limit will be either positive infinity (
To find out which one, we must test the one-sided limits:
- The limit from the right (approaching with a slightly larger number).
- The limit from the left (approaching with a slightly smaller number).
If both one-sided limits go to
Guided Practice Questions & Solutions
Find the limit:
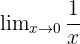
This is the classic example. The numerator is a non-zero constant (1), and the denominator is approaching 0. This is the k/0 form, so we must check the one-sided limits.
Limit from the right:
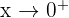
We test a number slightly larger than 0, like:
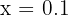
The expression becomes:
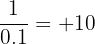
As x gets closer to 0 from the right, the denominator is a small positive number.
A (positive) / (small positive):
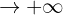
Limit from the left:
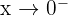
We test a number slightly smaller than 0, like:
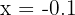
The expression becomes:
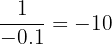
As x gets closer to 0 from the left, the denominator is a small negative number.
A (positive) / (small negative):
Answer: Since the left-side limit () and the right-side limit () do not match, the overall limit Does Not Exist (DNE).
Find the limit:
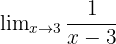
As x approaches 3, the numerator is 1 and the denominator approaches 0. This is the k/0 form. We check the one-sided limits.
Limit from the right:
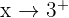
We test a number slightly larger than 3, like:
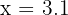
The denominator becomes:
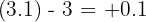
This is a small positive number. A positive numerator (1) over a small positive denominator approaches positive infinity:
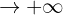
Limit from the left:
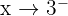
We test a number slightly smaller than 3, like:
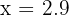
The denominator becomes:
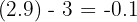
This is a small negative number. A positive numerator (1) over a small negative denominator approaches negative infinity:
Answer: The one-sided limits do not match. The limit Does Not Exist (DNE).
Find the limit:
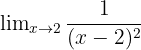
As x approaches 2, the numerator is 1 and the denominator approaches 0. This is the k/0 form.
Notice the denominator is squared. This means it will be positive, regardless of which side we approach from.
Limit from the right:
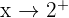
We test a number slightly larger than 2, like:
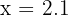
The denominator becomes:
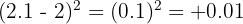
This is a small positive number. A positive numerator over a small positive denominator approaches positive infinity:
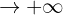
Limit from the left:
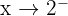
We test a number slightly smaller than 2, like:
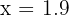
The denominator becomes:
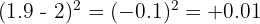
This is also a small positive number. The result again approaches positive infinity:
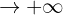
Answer: Since both the left-side and right-side limits approach , the overall limit is .
Find the limit:
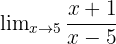
As x approaches 5:
The numerator approaches: 5 + 1 = 6 (a non-zero constant, k=6).
The denominator approaches: 5 - 5 = 0.
This is the k/0 form. We check the one-sided limits.
Limit from the right:
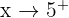
We test a number slightly larger than 5, like:
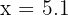
The numerator is positive:
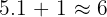
The denominator is positive:
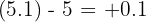
The result is (Positive) / (Positive):
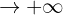
Limit from the left:
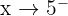
We test a number slightly smaller than 5, like:
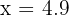
The numerator is positive:
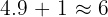
The denominator is negative:
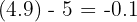
The result is (Positive) / (Negative):
Answer: The one-sided limits do not match. The limit Does Not Exist (DNE).
Find the limit:
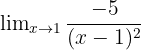
As x approaches 1:
The numerator is -5 (a non-zero constant, k = -5).
The denominator approaches 0.
This is the k/0 form. The denominator is squared, so it is always positive.
Limit from the right:
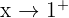
We test a number slightly larger than 1, like:
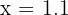
The numerator is negative (-5). The denominator is positive:
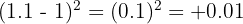
The result is (Negative) / (Positive):
Limit from the left:
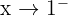
We test a number slightly smaller than 1, like:
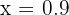
The numerator is negative (-5). The denominator is also positive:
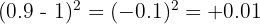
The result is (Negative) / (Positive):
Answer: Since both the left-side and right-side limits approach , the overall limit is .
Did you like this article? Rate it!
Loading...
Derivative of denominator is wrong
Good catch—thanks for pointing that out! We’ll double-check the derivative in that section and make any necessary corrections. Really appreciate you taking the time to flag it. 👍
Thank you
Thank you Abbas! Good luck with your studies!
With regard to the Zero Over a Number item, is there a mis-statement? It’s immediately followed by “If a number is divided by zero which means that the numerator is zero and the denominator is the number, then the result is zero.”
Hi Mark,
You’re absolutely right to raise the question — there does appear to be a misstatement in that sentence. The phrase “If a number is divided by zero, which means that the numerator is zero and the denominator is the number…” is indeed misleading and should be corrected.
To clarify:
Zero divided by a number (e.g. 0 ÷ 5) equals 0.
A number divided by zero (e.g. 5 ÷ 0) is undefined.
We’ll update the sentence to reflect the correct mathematical explanation. We appreciate you catching that and helping us improve the accuracy of the content!
There is more than one size of infinity, though. What if you multiply the infinity of the whole numbers (Aleph-0) by the infinity of the real numbers (fraktur-c)?
Thanks a lot to you for this essentiol article.
Hi Piyash! Thanks for your comment, great to hear that you found this useful!
Very nice