
Introduction
In mathematics, particularly in calculus, we often deal with limits. Usually, finding a limit is straightforward: you plug in the value and get an answer. However, sometimes we encounter expressions that don't give us a definitive answer immediately. These are called indeterminate forms.
An indeterminate form does not mean that the limit does not exist or that it is "undefined" (like dividing by zero). Instead, it means that the limit cannot be determined solely from the limits of the individual parts. The answer could be 0, 1, infinity, or any other real number, depending on the specific functions involved.
To solve these, mathematicians use specific techniques—such as algebraic manipulation or L'Hôpital's Rule (which uses differentiation)—to "break" the deadlock and find the true value.
Summary Table
Here is a quick reference guide to the seven forms.
| Type | Symbol | Description |
|---|---|---|
| Quotient | ∞ / ∞ | Numerator and denominator both grow without bound. |
| Quotient | 0 / 0 | Numerator and denominator both shrink to zero. |
| Difference | ∞ - ∞ | Subtraction of two infinite quantities. |
| Product | 0 × ∞ | Multiplication of a tiny number by a huge number. |
| Exponential | 0^0 | Zero raised to a power approaching zero. |
| Exponential | ∞^0 | Infinity raised to a power approaching zero. |
| Exponential | 1^∞ | A value near 1 raised to an infinite power. |
The 7 Types of Indeterminate Forms
There are seven specific forms that are considered indeterminate.
1. Infinity over Infinity
This occurs when both the numerator and the denominator of a fraction approach infinity. If you have a fraction:
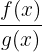
and both parts grow without bound, it is a "race" to infinity. If the top grows faster, the answer might be infinity. If the bottom grows faster, the answer might be 0. If they grow at the same rate, the answer could be a constant.
Form:

2. Infinity Minus Infinity
This happens when you subtract two quantities that are both approaching infinity. You might think that infinity minus infinity equals zero, but this is incorrect. Infinity is not a specific number; it is a concept of growth. If one "infinity" is much larger than the other "infinity," the result could be huge. If they are similar, it could be a constant.
Form:

3. Zero over Zero
This is perhaps the most common indeterminate form.
We know that 0÷5 = 0 and 5÷0 is undefined. But what about 0÷0?
In the context of limits, this represents a "tug of war" between the numerator (trying to make the fraction small) and the denominator (trying to make the fraction large). The result depends entirely on which function approaches zero faster.
Form:

4. Zero Times Infinity
Common logic suggests that "anything times zero is zero." However, logic also suggests that "anything times infinity is infinity." When we have a limit where one part approaches 0 and the other approaches infinity, we have a conflict. The result depends on whether the "zero" part is strong enough to pull the result down, or if the "infinity" part is strong enough to pull it up.
Form:

5. Zero to the Power of Zero
This form involves exponentiation.
Rule A says: "Zero to any power is 0."
Rule B says: "Any number to the power of 0 is 1."
When both the base and the exponent approach zero, these two rules conflict. The limit could end up being 1, 0, or something else entirely.
Form:

6. Infinity to the Power of Zero
Here, we have a base growing infinitely large, but an exponent shrinking to zero. We know that:

so the exponent tries to turn the number into 1. However, the base is becoming huge. This ambiguity makes it an indeterminate form.
Form:

7. One to the Power of Infinity
This is often the most confusing form for students.
We usually think that "1 to the power of anything is 1."
However, in calculus, the base is not exactly 1; it is approaching 1. If the base is a tiny bit larger than 1 (e.g., 1.000001) and you multiply it by itself an infinite number of times, it can grow into a massive number (like the mathematical constant e).
Form:













Derivative of denominator is wrong
Good catch—thanks for pointing that out! We’ll double-check the derivative in that section and make any necessary corrections. Really appreciate you taking the time to flag it. 👍
Thank you
Thank you Abbas! Good luck with your studies!
With regard to the Zero Over a Number item, is there a mis-statement? It’s immediately followed by “If a number is divided by zero which means that the numerator is zero and the denominator is the number, then the result is zero.”
Hi Mark,
You’re absolutely right to raise the question — there does appear to be a misstatement in that sentence. The phrase “If a number is divided by zero, which means that the numerator is zero and the denominator is the number…” is indeed misleading and should be corrected.
To clarify:
Zero divided by a number (e.g. 0 ÷ 5) equals 0.
A number divided by zero (e.g. 5 ÷ 0) is undefined.
We’ll update the sentence to reflect the correct mathematical explanation. We appreciate you catching that and helping us improve the accuracy of the content!
There is more than one size of infinity, though. What if you multiply the infinity of the whole numbers (Aleph-0) by the infinity of the real numbers (fraktur-c)?
Thanks a lot to you for this essentiol article.
Hi Piyash! Thanks for your comment, great to hear that you found this useful!
Very nice