Chapters
Infinity is one of the most fascinating and sometimes confusing concepts in mathematics. It allows us to explore ideas of endlessness, limitless growth, and values that defy ordinary calculation. In this article, we’ll explore what infinity is, how it’s represented, and its key properties. A summary table is included so you can easily reference the rules when working with infinity.

Introduction
The idea of infinity has intrigued mathematicians and philosophers for centuries. In simple terms, infinity describes something without end or limit. While not a number in the usual sense, infinity is a mathematical concept that helps us handle endless processes, very large values, or unbounded sets.
Infinity is not only important in mathematics, but also in physics, philosophy, and even computer science. Understanding its properties is essential for solving limits, working with series, and applying calculus techniques.
What is Infinity?
Infinity (∞) represents something that goes on forever. For example:
- The sequence of natural numbers {1, 2, 3, 4, …} never ends.
- A straight line contains an infinite number of points.
- The decimal expansion of 1/3 = 0.333... continues infinitely.
Mathematically, a set is called infinite if it can be put into a one-to-one correspondence with a subset of itself. For instance, the natural numbers {1, 2, 3, 4, …} can be paired with {2, 3, 4, 5, …}, showing both sets are equally infinite.
Symbol of Infinity
The infinity symbol ∞ (called a lemniscate) was introduced in 1657 by the English mathematician John Wallis. Its looping shape suggests something that never ends.
In calculus, infinity often appears in limits (e.g., as x → ∞) and in rules like L’Hôpital’s Rule, which deals with indeterminate forms involving infinity.
1. Mathematical Infinity – abstract numbers, sets, and calculus.
2. Physical Infinity – space, time, or the number of stars in the universe.
3. Metaphysical Infinity – philosophical and abstract concepts of the infinite.
Properties of Infinity
Infinity interacts with arithmetic in special ways. Some operations are straightforward, while others produce indeterminate forms (meaning they don’t have a well-defined answer). Zero is the mathematical opposite to infinity and is included in the table below as it too creates indeterminate forms.
Here’s a clear summary:
| Operation | Rule / Result | Notes |
|---|---|---|
| ∞ + number | ∞ | Infinity dominates addition. |
| ∞ + ∞ | ∞ | Still infinity. |
| ∞ - ∞ | Indeterminate | Cannot be determined. |
| ∞ × non-zero number | ∞ (if positive) | Keeps infinity. |
| ∞ × 0 | Indeterminate | Undefined result. |
| ∞ × ∞ | ∞ | Infinity grows. |
| number ÷ ∞ | 0 | A finite value becomes negligible. |
| ∞ ÷ number (non-zero) | ∞ | Infinity stays infinite. |
| ∞ ÷ ∞ | Indeterminate | Depends on context (limits). |
| 0 ÷ ∞ | 0 | Zero divided by infinity is still zero. |
| ∞ ÷ 0 | ∞ | Explosion toward infinity. |
| number^0 | 1 | Any non-zero number raised to zero is 1. |
| 0^0 | Indeterminate | Sometimes treated as 1, sometimes undefined. |
| ∞^0 | Indeterminate | No fixed result. |
| 0^positive number | 0 | Zero raised to a positive power is zero. |
| 0^negative number | ∞ | Reciprocal leads to infinity. |
| number^∞ | ∞ if number > 1, 0 if 0 < number < 1 | Growth vs. decay. |
| ∞^∞ | ∞ | Infinity raised to infinity is infinity. |
| 0^∞ | 0 | Zero raised to infinity stays zero. |
| 1^∞ | Indeterminate | Depends on the limit process. |
What Is Infinity Times Infinity?
When we talk about “infinity × infinity”, the meaning depends on the context:
- In arithmetic with real numbers, infinity (∞) isn’t a number — it’s a concept that represents something unbounded. So you can’t multiply it like ordinary numbers. Saying “∞ × ∞” is not a well-defined real number.
- In calculus or limit notation, if something grows without bound and you multiply two such unbounded quantities, the result is said to grow without bound faster — we might loosely say it’s “∞”.
Formally: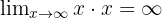
So, ∞ × ∞ = ∞ in that symbolic sense (meaning “still infinite,” not a specific value).
So in this sense, “infinity times infinity” is the same infinity.
- In normal arithmetic → undefined.
- In limits → still ∞ (grows without bound).
What Is Infinity Plus Infinity?
- Arithmetic: Infinity ∞ isn’t a real number — so: ∞+∞ is undefined in ordinary arithmetic
- Calculus/Limits: In limit notation, if two quantities each grow without bound, their sum also grows without bound:
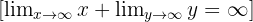
So symbolically, we write: ∞+∞=∞
This means “still infinite,” not a larger or different infinity.
Why These Properties Matter
Understanding how infinity behaves is essential in:
- Limits (e.g., lim x→∞ f(x))
- Calculus (handling infinite series or improper integrals)
- Real-world applications (modelling populations, time, or unbounded growth)
Infinity helps us formalize ideas of growth without end and manage operations that would otherwise be impossible with finite numbers.
Conclusion
Infinity isn’t just a “big number.” It’s a mathematical concept that lets us describe the endless, the unbounded, and the limitless. By learning its properties, we can better navigate topics like calculus, series, and limits.
Keep this table handy—it’s your quick reference guide whenever infinity shows up in a problem!












Derivative of denominator is wrong
Good catch—thanks for pointing that out! We’ll double-check the derivative in that section and make any necessary corrections. Really appreciate you taking the time to flag it. 👍
Thank you
Thank you Abbas! Good luck with your studies!
With regard to the Zero Over a Number item, is there a mis-statement? It’s immediately followed by “If a number is divided by zero which means that the numerator is zero and the denominator is the number, then the result is zero.”
Hi Mark,
You’re absolutely right to raise the question — there does appear to be a misstatement in that sentence. The phrase “If a number is divided by zero, which means that the numerator is zero and the denominator is the number…” is indeed misleading and should be corrected.
To clarify:
Zero divided by a number (e.g. 0 ÷ 5) equals 0.
A number divided by zero (e.g. 5 ÷ 0) is undefined.
We’ll update the sentence to reflect the correct mathematical explanation. We appreciate you catching that and helping us improve the accuracy of the content!
There is more than one size of infinity, though. What if you multiply the infinity of the whole numbers (Aleph-0) by the infinity of the real numbers (fraktur-c)?
Thanks a lot to you for this essentiol article.
Hi Piyash! Thanks for your comment, great to hear that you found this useful!
Very nice