To understand discontinuity, you should know what is continuity of a function. If a function doesn't have any anomalous point or breaking point, it means it is a continuous function. However, not all functions are continuous, we call them discontinuous function. A discontinuous function is a function that changes its behaviour after some time. One of the best examples of discontinuous function is the piecewise function. A piecewise function is a type of function that is defined by many sub-functions with a certain interval. In simple words, a piecewise function contains functions of its own with its own domain. These sub-functions are the indication that there are some discontinuity points between them and from those points, the function gives a different output for different inputs.
One thing is clear, piecewise functions are discontinuous function but which type of discontinuity? There are three types of discontinuity and they are:
- Point/Removal discontinuity
- Jump discontinuity
- Asymptotic discontinuity
Piecewise functions are mostly jumped discontinuity function. These types of discontinuity are very detailed and deserve their own resources and that is why, in this lecture, we will discuss jump discontinuity.
What is Jump Discontinuity?
Imagine a graph of a function that has two sub-functions which are:
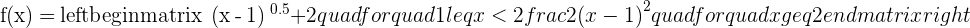
Let's make a graph of the above piecewise function.
Notice something? At point 
, there is a jump. The first sub-function (i.e. 
) ended before point and from the same point, the second sub-function (i.e.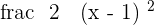 
) starts and goes till infinity. That means that at point , there is a jump in sub-functions. In conclusion, if a function behaves differently not just on a specific point but it has its own domain, we call it a jump discontinuity.
How To Check Jump Discontinuity?
The best way to check jump discontinuity is to apply limits on the left and right sides of the limits. If they both are equal to each other that means there is no jump discontinuity, however, if they are not equal that indicates jump discontinuity. For example, we have a piecewise function:
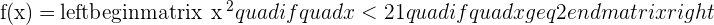
If the left and right sides of the limits at 
exist, and they are finite but not equal, then at there is a jump discontinuity or a step discontinuity.
Did you like this article? Rate it!
Loading...
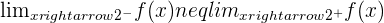
Derivative of denominator is wrong
Good catch—thanks for pointing that out! We’ll double-check the derivative in that section and make any necessary corrections. Really appreciate you taking the time to flag it. 👍
Thank you
Thank you Abbas! Good luck with your studies!
With regard to the Zero Over a Number item, is there a mis-statement? It’s immediately followed by “If a number is divided by zero which means that the numerator is zero and the denominator is the number, then the result is zero.”
Hi Mark,
You’re absolutely right to raise the question — there does appear to be a misstatement in that sentence. The phrase “If a number is divided by zero, which means that the numerator is zero and the denominator is the number…” is indeed misleading and should be corrected.
To clarify:
Zero divided by a number (e.g. 0 ÷ 5) equals 0.
A number divided by zero (e.g. 5 ÷ 0) is undefined.
We’ll update the sentence to reflect the correct mathematical explanation. We appreciate you catching that and helping us improve the accuracy of the content!
There is more than one size of infinity, though. What if you multiply the infinity of the whole numbers (Aleph-0) by the infinity of the real numbers (fraktur-c)?
Thanks a lot to you for this essentiol article.
Hi Piyash! Thanks for your comment, great to hear that you found this useful!
Very nice