Chapters
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 8
- Exercise 9
- Exercise 10
- Exercise 11
- Exercise 12
- Solution of exercise 1
- Solution of exercise 2
- Solution of exercise 3
- Solution of exercise 4
- Solution of exercise 5
- Solution of exercise 6
- Solution of exercise 7
- Solution of exercise 8
- Solution of exercise 9
- Solution of exercise 10
- Solution of exercise 11
- Solution of exercise 12

Exercise 1
Prove that the function 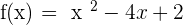 intersects the x-axis on the interval
intersects the x-axis on the interval  . Can the same be said for the function:
. Can the same be said for the function:  ?
?
Exercise 2
Given the function:

Can it be said that f(x) is bounded in the interval 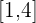 ?
?
Exercise 3
Given the function  . Can it be said that the function exists for all values in the interval
. Can it be said that the function exists for all values in the interval 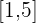 ?
?
Exercise 4
Prove that the equation: 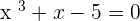 , has at least one solution
, has at least one solution  such that
such that  .
.
Exercise 5
Given the function  . Can it be said that there is at least one point, c, inside the interval
. Can it be said that there is at least one point, c, inside the interval 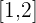 which verifies that
which verifies that 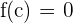 ?
?
Exercise 6
Prove that the polynomial function 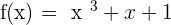 has a value of zero between
has a value of zero between  and
and  .
.
Exercise 7
Prove that the equation  has at least one real solution.
has at least one real solution.
Exercise 8
Prove that there is a real number, x, such that 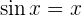 .
.
Exercise 9
Given the function:
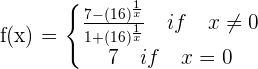
Prove that there is a point in the open interval  in which the function
in which the function  has a value of
has a value of  .
.
Exercise 10
Given the function 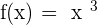 , determine if it is bounded superiorly and inferiorly in the interval
, determine if it is bounded superiorly and inferiorly in the interval  and indicate if it reaches its maximum and minimum values within this interval.
and indicate if it reaches its maximum and minimum values within this interval.
Exercise 11
Prove that the function  is continuous at
is continuous at  and prove that there exists at least one real root of the equation
and prove that there exists at least one real root of the equation 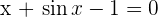 .
.
Exercise 12
f and g are two continuous functions in  and such that
and such that  and
and  . Prove the existance of c withinin
. Prove the existance of c withinin  such that
such that 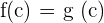 .
.
Solution of exercise 1
Prove that the function 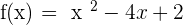 intersects the x-axis on the interval
intersects the x-axis on the interval  . Can the same be said for the function:
. Can the same be said for the function:  ?
?
The first function is continuous at  .
.
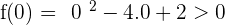 .
.
 .
.
Since it verifies the intermediate value theorem, at least one c belongs to the interval 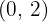 and intersects the x-axis.
and intersects the x-axis.
We cannot confirm the same of the second function because it is not continuous at  .
.
Solution of exercise 2
Given the function:

Can it be said that f(x) is bounded in the interval 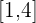 ?
?
Since f(x) is not continuous at  , the function is not continuous in the closed interval
, the function is not continuous in the closed interval 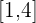 , as a result, it cannot be said that the function is bounded in that interval.
, as a result, it cannot be said that the function is bounded in that interval.
Solution of exercise 3
Given the function  . Can it be said that the function exists for all values in the interval
. Can it be said that the function exists for all values in the interval 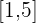 ?
?
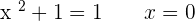
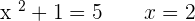
The function is continuous at  since it is a polynomial function.
since it is a polynomial function.
It is in the interval  as it is verified that
as it is verified that  and
and 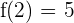 .
.
Since it verifies the intermediate value theorem, the function exists at all values in the interval 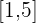 .
.
Solution of exercise 4
Prove that the equation: 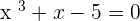 , has at least one solution
, has at least one solution  such that
such that  .
.
f(x) is continuous in 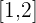
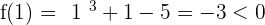
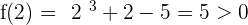
Since it verifies the Bolzano's Theorem, there is c 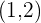 such that:
such that:
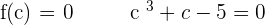
Therefore there is at least one real solution to the equation 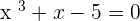 .
.
Solution of exercise 5
Given the function  . Can it be said that there is at least one point, c, inside the interval
. Can it be said that there is at least one point, c, inside the interval 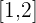 which verifies that
which verifies that 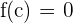 ?
?
f(x) is continuous in  .
.
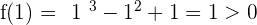
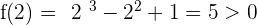
The Bolzano theorem cannot be applied because it does not change sign.
Solution of exercise 6
Prove that the polynomial function 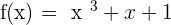 has a value of zero between
has a value of zero between  and
and  .
.
 is a polynomial and therefore is continuous in the interval
is a polynomial and therefore is continuous in the interval  .
.
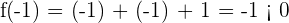
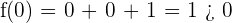 .
.
There is a 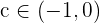 such that
such that 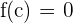
Solution of exercise 7
Prove that the equation  has at least one real solution.
has at least one real solution.
The function is continuous in the interval 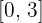 .
.
 .
.
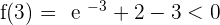 .
.
Since it verifies Bolzano's theorem, there is 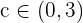 such that:
such that:

Therefore there is at least one real solution to the equation  .
.
Solution of exercise 8
Prove that there is a real number, x, such that 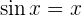 .
.
Consider the function  .
.
It is continuous at  .
.


There is a  such that:
such that:

Therefore, there is at least one real solution to the equation 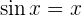 .
.
Solution of exercise 9
Given the function:
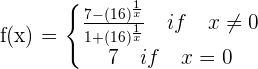
Prove that there is a point in the open interval  in which the function
in which the function  has a value of
has a value of  .
.
The exponential function is positive at  , therefore the denominator of the function cannot be annulled.
, therefore the denominator of the function cannot be annulled.
There is only doubt of the continuity at  , which is out of the interval being studied, therefore
, which is out of the interval being studied, therefore  is continuous in
is continuous in 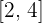 .
.
Consider the function g defined by 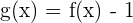 .
.
g is continuous on the interval 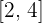 .
.
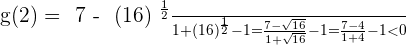

Since it verifies the intermediate value theorem, there is a 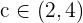 such that:
such that:
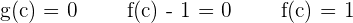
Solution of exercise 10
Given the function 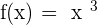 , determine if it is bounded superiorly and inferiorly in the interval
, determine if it is bounded superiorly and inferiorly in the interval  and indicate if it reaches its maximum and minimum values within this interval.
and indicate if it reaches its maximum and minimum values within this interval.
The function is continuous in the interval  , as a result, it can be affirmed that it is bounded in that interval.
, as a result, it can be affirmed that it is bounded in that interval.
As well as being continuous in the interval  , it has fulfilled the extreme value theorem, which affirms that it attains at least one maximum and absolute minimum in the interval
, it has fulfilled the extreme value theorem, which affirms that it attains at least one maximum and absolute minimum in the interval  .
.
Solution of exercise 11
Prove that the function  is continuous at
is continuous at  and prove that there exists at least one real root of the equation
and prove that there exists at least one real root of the equation 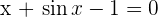 .
.
The function is continuous since it is the sum of continuous functions.
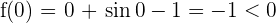

Since it verifies the intermediate value theorem, there is a 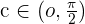 such that:
such that:

Therefore, there is at least one real solution to the equation 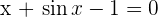 .
.
Solution of exercise 12
f and g are two continuous functions in  and such that
and such that  and
and  . Prove the existance of c withinin
. Prove the existance of c withinin  such that
such that 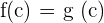 .
.
h is the function defined by 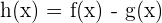 .
.
Since f and g are continuous in  , the function h also is.
, the function h also is.
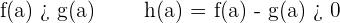
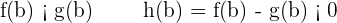
Since it verifies the intermediate value theorem, there is a 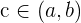 such that:
such that:
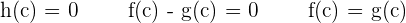













Derivative of denominator is wrong
Good catch—thanks for pointing that out! We’ll double-check the derivative in that section and make any necessary corrections. Really appreciate you taking the time to flag it. 👍
Thank you
Thank you Abbas! Good luck with your studies!
With regard to the Zero Over a Number item, is there a mis-statement? It’s immediately followed by “If a number is divided by zero which means that the numerator is zero and the denominator is the number, then the result is zero.”
Hi Mark,
You’re absolutely right to raise the question — there does appear to be a misstatement in that sentence. The phrase “If a number is divided by zero, which means that the numerator is zero and the denominator is the number…” is indeed misleading and should be corrected.
To clarify:
Zero divided by a number (e.g. 0 ÷ 5) equals 0.
A number divided by zero (e.g. 5 ÷ 0) is undefined.
We’ll update the sentence to reflect the correct mathematical explanation. We appreciate you catching that and helping us improve the accuracy of the content!
There is more than one size of infinity, though. What if you multiply the infinity of the whole numbers (Aleph-0) by the infinity of the real numbers (fraktur-c)?
Thanks a lot to you for this essentiol article.
Hi Piyash! Thanks for your comment, great to hear that you found this useful!
Very nice