Chapters
In mathematics, continuous functions are very important because of their unique functions and applications in many other fields. Every function is not continuous. If a function is non-continuous at a specific point in its domain, then we say that the function has a discontinuity at that point. The set of all discontinuous points of a given function can form a discrete set, a dense set, or may even constitute the entire domain of the function. There are two kinds of discontinuities in a function: removable and non-removable. In this article, we will discuss what is removable discontinuity, how it differs from non-removable discontinuity, how to identify it in a given function and how to plot it on the graph. So, let us get started.

What is Removable Discontinuity?
A removable discontinuity is defined as follows:
A point on the graph that is undefined or is unfit for the rest of the graph is known as a removable discontinuity
You can identify this point by seeing a gap where this point is located. On the graph, a removable discontinuity is marked by an open circle to specify the point where the graph is undefined.
Difference Between Removable and Non-Removable Discontinuities
The functions that are not continuous at any value of x either have a removable or a non-removable discontinuity. If the limit does not exist at a specific point, then the discontinuity is non-removable at that point. On the other hand, if adjusting a function's value at a specific point of discontinuity will give a continuous function, then we say that the discontinuity is removable at that point.
How to Solve Removable Discontinuity?
Follow these steps to solve removable discontinuities.
Step 1 - Factor out the numerator and the denominator
Step 2 - Determine the common factors in the numerator and the denominator
Step 3 - Set the common factors equal to zero and find the value of x.
Step 4 - Plot the graph and mark the point with a hole
In the next section, we will solve some examples in which we will find the removable discontinuity of a function and plot it on the graph.
Example 1
Find the removable discontinuity of the following function:
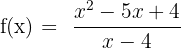
Solution
Follow these steps to identify the removable discontinuity of the above function.
Step 1 - Factor out the numerator and the denominator
Find the factors of the numerator and the denominator. The denominator cannot be factored further, but we can factor the numerator.
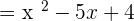
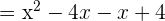
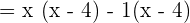
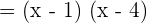
Step 2 - Determine the common factors in the numerator and the denominator
As we can see that the common factor in the numerator and the denominator is (x - 4). We can rewrite the original function like this:
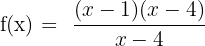
Step 3 - Set the common factors equal to zero and find the value of x
Now, we have identified the common factor which is x - 4. We need to set it equal to zero to get the removable discontinuity.
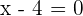

Hence, the removable discontinuity of the function is at the point x = 4.
Step 4 - Plot the graph and mark the point with a hole
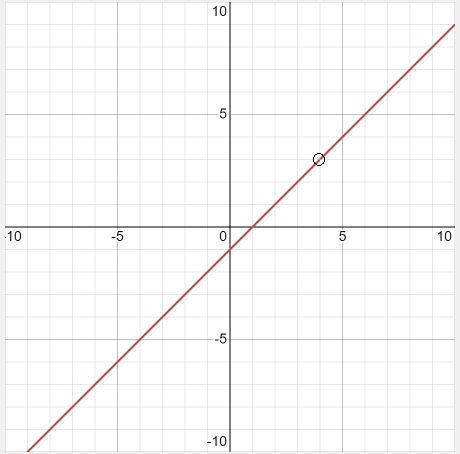
Example 2
Find the removable discontinuity of the following function:
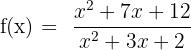
Solution
Follow these steps to identify the removable discontinuity of the above function.
Step 1 - Factor out the numerator and the denominator
Find the factors of the numerator and the denominator. Both the numerator and the denominator can be factored in this example.
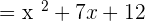
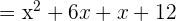
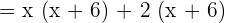
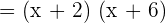
Now, we will factor out the denominator using the same above procedure as shown below:
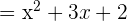
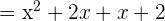
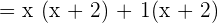

Step 2 - Determine the common factors in the numerator and the denominator
As we can see that the common factor in the numerator and the denominator is (x + 4). We can rewrite the original function like this:
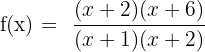
Step 3 - Set the common factors equal to zero and find the value of x
Now, we have identified the common factor which is x + 2. We need to set it equal to zero to get the removable discontinuity.

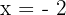
Hence, the removable discontinuity of the function is at the point x = - 2.
Step 4 - Plot the graph and mark the point with a hole

Example 3
Find the removable discontinuity of the following function:
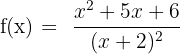
Solution
Follow these steps to identify the removable discontinuity of the above function.
Step 1 - Factor out the numerator and the denominator
Find the factors of the numerator and the denominator. Both the numerator and the denominator can be factored.
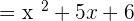
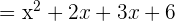
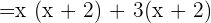
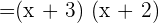
Now, we will factor the denominator like this:
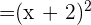
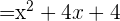
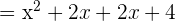
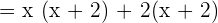
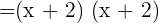
Step 2 - Determine the common factors in the numerator and the denominator
As we can see that the common factor in the numerator and the denominator is (x + 2) . We can rewrite the original function like this:
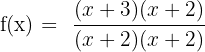
Step 3 - Set the common factors equal to zero and find the value of x
Now, we have identified the common factor which is x + 2. We need to set it equal to zero to get the removable discontinuity.


Hence, the removable discontinuity of the function is at the point x = -2.
Step 4 - Plot the graph and mark the point with a hole

Example 4
Find the removable discontinuity of the following function:
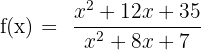
Solution
Follow these steps to identify the removable discontinuity of the above function.
Step 1 - Factor out the numerator and the denominator
Find the factors of the numerator and the denominator. Both the numerator and the denominator can be factored in this example.
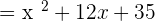
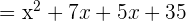
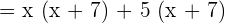
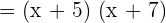
Now, we will factor out the denominator using the same above procedure as shown below:
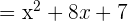
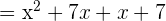
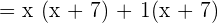
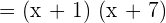
Step 2 - Determine the common factors in the numerator and the denominator
As we can see that the common factor in the numerator and the denominator is (x + 7). We can rewrite the original function like this:
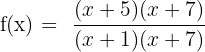
Step 3 - Set the common factors equal to zero and find the value of x
Now, we have identified the common factor which is x + 2. We need to set it equal to zero to get the removable discontinuity.
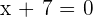
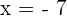
Hence, the removable discontinuity of the function is at the point x = - 7.
Step 4 - Plot the graph and mark the point with a hole














Derivative of denominator is wrong
Good catch—thanks for pointing that out! We’ll double-check the derivative in that section and make any necessary corrections. Really appreciate you taking the time to flag it. 👍
Thank you
Thank you Abbas! Good luck with your studies!
With regard to the Zero Over a Number item, is there a mis-statement? It’s immediately followed by “If a number is divided by zero which means that the numerator is zero and the denominator is the number, then the result is zero.”
Hi Mark,
You’re absolutely right to raise the question — there does appear to be a misstatement in that sentence. The phrase “If a number is divided by zero, which means that the numerator is zero and the denominator is the number…” is indeed misleading and should be corrected.
To clarify:
Zero divided by a number (e.g. 0 ÷ 5) equals 0.
A number divided by zero (e.g. 5 ÷ 0) is undefined.
We’ll update the sentence to reflect the correct mathematical explanation. We appreciate you catching that and helping us improve the accuracy of the content!
There is more than one size of infinity, though. What if you multiply the infinity of the whole numbers (Aleph-0) by the infinity of the real numbers (fraktur-c)?
Thanks a lot to you for this essentiol article.
Hi Piyash! Thanks for your comment, great to hear that you found this useful!
Very nice