Chapters

Zero Over Zero
Let’s take a look at what zero over zero looks like:

This is known as an indeterminate form, because it is unknown. In fact, any number divided by zero is unknown. Take a look at some examples.

When would we encounter a situation like this? Say you want to find the limit of the following function as it approaches zero:

When we plug zero into this function, we see that it takes on the indeterminate form of zero over zero. To solve this, let’s take a look at an example.
Example
Take the following equation.

Let’s take the limit of the following function as it approaches 2.

To take the limit, we first replace all the x values by our a value of 2.

The result gives us zero over zero.
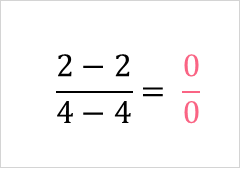
As we discussed in the previous section, zero over zero is undefined. When we take the limit by approaching 2 from the right and left side, we see what happens.
| x | y |
| 2.1 | -0.47619 |
| 2.01 | -0.49751 |
| 2.001 | -0.49975 |
| 2.0001 | -0.49998 |
We start to approach a limit, -0.5, as x approaches 2. However what’s another way we can do this without having to plug in a lot of different x values? In order to solve this, we should review what limits are.
Limits Summary
When you take the limit of a function, you want to know what value it approaches when x reaches a specific value. Let’s review the notation.
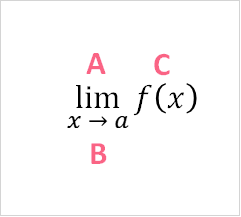
| A | lim | Symbol for the limit | lim (5x+3) |
| B | x -> a | As x approaches a specified value a | 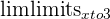 |
| C | f(x) | The function we’re finding the limit for | 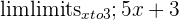 |
When you take the limit of an equation, the standard method is to simply plug in the a value into the function. Take this example.

| Step 1 | Identify the a value | a = 3 |
| Step 2 | Replace the x values with a | 5(3) + 3 = 15 + 3 |
| Step 3 | Solve for the limit | 18 |
Keep in mind, there are two ways to approach a limit.
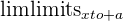 |  |
| Approach from right side | Approach from left side |
Indeterminate Forms
Indeterminate forms, as mentioned earlier, are expressions whose values are unknown. Let’s take a look at the most common examples.

| A | Fraction |
| B | Standard |
| C | Power |
You can’t find the limit for indeterminate forms because their true value is unknown. Often times, you will run into functions which result in indeterminate forms. Take a look at the examples below.
 | 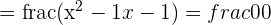 |
 |  |
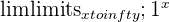 | 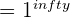 |
In these instances, you can either try to factor the function so that it doesn’t result in an indeterminate form, or use l’Hopital’s rule.
L’Hopital Rule
Let’s take our previous example, which resulted in the indeterminate form zero over zero.

L’Hopital’s rule states that when we have two functions divided by each other, the result is the same if we take the derivative of each function and divide them.

This rule allows us to differentiate the first and second functions almost as if we were differentiating two separate functions. Here are the conditions in order to use this rule:
| Limit must exist | The limit must exist at the new differentiated function. |
| Differentiable at a | The functions should be differentiable as it approaches a from the right or left |
Solving Zero over Zero
In order to find the limit of an indeterminate form, we will take the following example.

When we plug in zero into the function, we end up with the indeterminate form zero over zero.
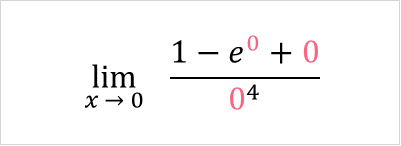
Here, we can apply l’Hopital’s rule for finding the limit.
Step 1
The first step in using l’Hopital’s rule for finding the limit of a function is to find the derivative of the numerator and the denominator independently of one another.
Meaning, instead of taking the derivative of the entire rational function, we can start by simply taking the derivative of the numerator.

You can find the derivative of the function by following the rules for derivatives.
Step 2
The next step is to take the derivative of the denominator. Again, we use the rules for derivatives to help us out.

As you can see, we now have the derivative of the top function and the derivative for the bottom function.
Step 3
Now that we have taken the derivative of the numerator independently of the denominator, we can now try plugging our value a into the equation again to find the limit for the function.

As you can see, we get the indeterminate form zero over zero again. Let’s take a look at the general method for using l’Hopital’s rule to figure out what to do next.
| Step 1 | You have an indeterminate form |
| Step 2 | Take the derivative of the numerator and denominator independently of one another |
| Step 3 | Plug the a value back in to get the limit of the function. If this results in another indeterminate form, continue to step 4. |
| Step 4 | Repeat steps 2 and 3. If you keep getting an indeterminate form, you will most likely have to use the factoring method to find the limit. |
Step 4
We will now take the derivative of the top and bottom function again.

Now, we find the limit of this function by plugging zero in again.

The result is 1 over 4. This is good news, we have found the limit! If this would have resulted in another indeterminate form, such as zero over zero again, we would have had to try to use a different method before using l’Hopital’s rule.













Derivative of denominator is wrong
Good catch—thanks for pointing that out! We’ll double-check the derivative in that section and make any necessary corrections. Really appreciate you taking the time to flag it. 👍
Thank you
Thank you Abbas! Good luck with your studies!
With regard to the Zero Over a Number item, is there a mis-statement? It’s immediately followed by “If a number is divided by zero which means that the numerator is zero and the denominator is the number, then the result is zero.”
Hi Mark,
You’re absolutely right to raise the question — there does appear to be a misstatement in that sentence. The phrase “If a number is divided by zero, which means that the numerator is zero and the denominator is the number…” is indeed misleading and should be corrected.
To clarify:
Zero divided by a number (e.g. 0 ÷ 5) equals 0.
A number divided by zero (e.g. 5 ÷ 0) is undefined.
We’ll update the sentence to reflect the correct mathematical explanation. We appreciate you catching that and helping us improve the accuracy of the content!
There is more than one size of infinity, though. What if you multiply the infinity of the whole numbers (Aleph-0) by the infinity of the real numbers (fraktur-c)?
Thanks a lot to you for this essentiol article.
Hi Piyash! Thanks for your comment, great to hear that you found this useful!
Very nice