Chapters

What is a Derivative?
A derivative of a function is an instantaneous rate of change of the function at a specific point. The process of computing a derivative is known as differentiation. Finding derivatives is one of the fundamental concepts of calculus especially its sub-branch differential calculus.
The opposite of the derivative is known as an antiderivative. Since integral and antiderivatives of the functions are closely associated, hence we often use these terms interchangeably. The process of computing integral of a function is known as integration. Integration is the inverse of differentiation. In other words, we can say that a derivative of a function is the rate at which y value of the function changes with respect to the variable x.
There are more than one method to represent the derivative of the function mathematically. A derivative can be denoted in fractional form like this:
 or
or 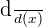 .
.
Alternatively, you can denote a derivative like this:
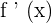
The derivative of a function can be computed using the limit formula which is given below:
 f ' (x) = \lim_{h \rightarrow 0} \frac {f (a + h) - f(a) } {h}
f ' (x) = \lim_{h \rightarrow 0} \frac {f (a + h) - f(a) } {h} 
We can find multiple derivatives of the same function. When we compute the derivative of a function, it is known as the first derivative. Similarly, when we differentiate the first derivative further we get the second derivative and when the second derivative is differentiated further, we get the third derivative and so on. The second and third derivatives of the functions are also known as higher order derivatives.
In this article, we will see some of the basic derivative rules and formulas or rules of differentiation. These rules are simple, and you can memorize them as they will be helpful in computing the derivatives of the functions. Sometimes when the functions are complex, we employ multiple derivative rules simultaneously.
Derivative of a Constant
The derivative of the constant is zero. For example, consider the function 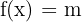 , where m is a constant. The derivative of this function will denoted by
, where m is a constant. The derivative of this function will denoted by 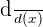 or
or 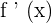 and is equal to zero.
and is equal to zero.
Derivative of x
The derivative of the variable  is equal to 1. For example, the function
is equal to 1. For example, the function  has the derivative equal to 1. It can be denoted as follows:
has the derivative equal to 1. It can be denoted as follows:

Derivative of a Constant Multiple
If a constant is multiplied with a function, then the general form of its derivative is given as follows.
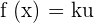
Here, k is a constant and u is a function
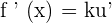
Example
Find the derivatove of the function 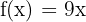
Solution
Using the above rule, we can differentiate this function like this:
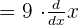
Since, derivative of the variable  is equal to 1, hence the derivative of the function
is equal to 1, hence the derivative of the function 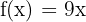 is equal to
is equal to  . It can be represented mathematically as:
. It can be represented mathematically as:
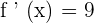
Derivative of a Linear Function
The derivative of the linear function is equal to its slope. A linear function can be written in general form, point slope form and slope intercept form. The slope intercept form of the linear function is  . Here, m is the slope of a line,
. Here, m is the slope of a line,  is the variable and b is the constant of the function. Any function which is written in the slope intercept form has the derivative equal to
is the variable and b is the constant of the function. Any function which is written in the slope intercept form has the derivative equal to  . Let us consider the following example:
. Let us consider the following example:
Find the derivative of the function 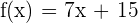
Since the above function is in the slope intercept form  , hence the slope of the above function is 7. The derivative of the function is also equal to its slope and can be written as follows:
, hence the slope of the above function is 7. The derivative of the function is also equal to its slope and can be written as follows:
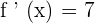
Power Rule
The formula for finding the derivative of an exponential function is given below:
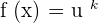
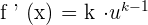
Consider the following example to know how to find the derivative of a power function.
Example
Find the derivative of the function 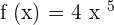
Solution
We can use two basic derivative rules, while differentiating the above function. First since the function is multiplied by a constant 4, hence we can write the function as a product of 4 and 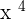 like this:
like this:

Now, we need to find the derivative of 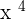 because when a constant is multiplied by a function, we find the derivative of the function and multiply the constant with it.
because when a constant is multiplied by a function, we find the derivative of the function and multiply the constant with it.

Apply the derivative power rule 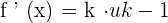 here to find the derivative of
here to find the derivative of 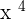 .
.
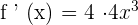
Simplifying the above derivative function will give us the following:
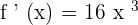
Derivative of a Square Root
The formula for finding the derivative of a square root function is given below:
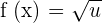
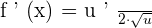
Example 1
Find the derivative of the function 
Solution
Find out how to differentiate the above function by following these steps.
Step 1 - First, find the derivative of the term inside the square root function. Inside the square root, we are given a variable  . The derivative of the variable
. The derivative of the variable  is equal to 1.
is equal to 1.
Step 2 - Substituting the value of the function and its derivative in the formula 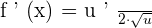 will give us the following derivative of a function:
will give us the following derivative of a function:

Example 2
Find the derivative of the function 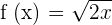
Solution
Again, we need to solve this function step wise.
Step 1 - Find the derivative of the term  as it is inside the square root function. While finding the derivative of the constant multiplied by the function, we can rewrite the function as:
as it is inside the square root function. While finding the derivative of the constant multiplied by the function, we can rewrite the function as:
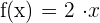
We need to find the derivative of the function and multiply it by the constant. Since the derivative of the variable is equal to 1, hence the derivative of the above function is equal to 2.
Step 2 - Substitute the value of the derivative and the original function in the formula 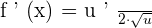 .
.
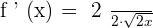
We should always write the answer in the most simplified form. Since in the above function 2 is the common number both in the numerator and denominator, hence we will cancel out this constant and write the answer as:
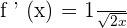
Derivative of a Reciprocal
The derivative of the reciprocal is expressed mathematically as:
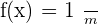

Consider the following example to know how to use the above reciprocal rule to find the derivative of a function.
Example
Find the derivative of the function 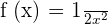 .
.
Solution
Follow these steps to find the derivative of the above function.
Step 1 - First, find the derivative of the term in the denominator.  can be written as the product of constant and exponent like this:
can be written as the product of constant and exponent like this:
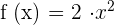
The derivative of 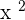 is equal to 2x, so the derivative of
is equal to 2x, so the derivative of 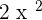 is equal to 4x.
is equal to 4x.
Step 2 - Take the square of the denominator. We have  in the denominator. Squaring
in the denominator. Squaring  will give us
will give us 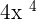 .
.
Step 3 - Substitute the values from step 1 and step 2 in the derivative formula of the reciprocal  to get the derivative of the entire function.
to get the derivative of the entire function.

We will write the final answer in the simplified form because the terms in the numerator and the denominator can be divided by each other.

Derivative of a Root
So far we have learnt how to find the derivative of a square root function. Now, we will see how to find out the derivative of a root function. The general formula used to compute the derivative of the root function is given below:
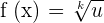

Example 1
Find the derivative of the function 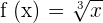 .
.
Solution
Follow these steps to find the derivative of the above root function.
Step 1 - Find the derivative of the term inside the root function. In the above example, the term inside the root function is  , hence the derivative of the function
, hence the derivative of the function  is equal to 1.
is equal to 1.
Step 2 - See the value of k in the above function. The value of k is 3.
Step 3 - Find 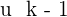 . In the above function,
. In the above function, 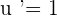 . Hence, we will write
. Hence, we will write  as
as 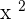 .
.
Step 4 - Substitute the values of k , u ' and 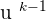 in the formula
in the formula 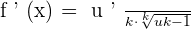 to get the derivative of the function.
to get the derivative of the function.

We will write the above derivative function in its most simplified form like this:
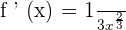
Example 2
Find the derivative of the function 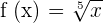
Solution
Follow these steps to find the derivative of the above root function.
Step 1 - Find the derivative of the term inside the root function. In the above example, the term inside the root function is  , hence the derivative of the function
, hence the derivative of the function  is equal to 1.
is equal to 1.
Step 2 - See the value of k in the above function. The value of k is 5.
Step 3 - Find  . In the above function,
. In the above function,  . Hence, we will write
. Hence, we will write  as
as 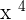 .
.
Step 4 - Substitute the values of k , u ' and 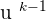 in the formula
in the formula  to get the derivative of the function.
to get the derivative of the function.
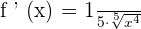
We will write the above derivative function in its most simplified form like this:

Sum or Difference
The derivative of the sum or difference is calculated as follows:

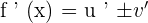
Example 1
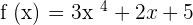 .
.Solution
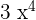 , we need to use the power rule.
, we need to use the power rule. 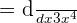
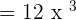
The derivative of the second term  is 2 and the derivative of the last term is 0 because it is a constant. Hence, the derivative of the entire function can be written as:
is 2 and the derivative of the last term is 0 because it is a constant. Hence, the derivative of the entire function can be written as:

Example 2
Find the derivative of the function 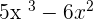 .
.
Solution
The derivative of the first term is 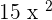 . Similarly, the derivative of the second term is
. Similarly, the derivative of the second term is 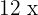 . We will use the derivative difference rule to write the derivative of the whole function like this:
. We will use the derivative difference rule to write the derivative of the whole function like this:

The arithmetic sign of subtraction will remain the same as per the derivative difference rule.
Derivative of Basic Trigonometric Functions
The derivatives of some basic trigonometric function as given below:
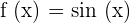
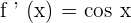
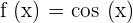

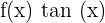
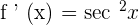
Summarise with AI:













Like the explanation, want to rearn more. Really enjoying the documents received.