Chapters
- What is a Derivative?
- Derivative of a Constant
- Derivative of a Constant Multiple
- Derivative of x
- Derivative Power Rule
- Derivative of a Root
- Derivative of a Sum or Difference
- Derivative Product Rule
- Derivative Quotient Rule
- Derivative Reciprocal Rule
- Derivative of an Exponential Function
- Derivative of a Logarithmic Function
- Derivative of a Sine Function
- Derivative of a Cosine Function
- Derivative of a Tangent Function
- Derivative Chain Rule

What is a Derivative?
The derivative is defined as an instantaneous rate of change of a function at any given point. This instantaneous rate of change is also known as a slope. The general notation of a derivative function is given by the following function:

In other words, we can say that a derivative of a function is the rate of change in y with respect to x. The integration of a function is inverse of the derivative. The process of calculating a derivative is known as differentiation. In this article, we will learn some of the derivative rules or rules of differentiation along with the relevant examples.
Derivative of a Constant
The derivative of a constant function is equal to zero.
Example
If a is a constant, then the following function will have the zero derivative:

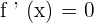
Here, we have represented derivative of function by 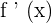 . We can also represent a derivative function by
. We can also represent a derivative function by 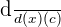 . Both notations are used to represent the derivative of a function.
. Both notations are used to represent the derivative of a function.
Derivative of a Constant Multiple
If we have to find the derivative of a function in which the constant is multiplied by the function, then we take THE derivative of the function and multiply the constant with it. The general notation of this rule is given below:
If  , then
, then 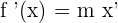
Example 1
Find the derivative of the function 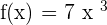 .
.
Solution
In the above function, a constant 7 is multiplied by the variable  . So, first we will write 7 as it is and take the derivative of the cubic variable
. So, first we will write 7 as it is and take the derivative of the cubic variable  inside the parentheses.
inside the parentheses.
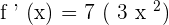
To take the derivative of the cubic function 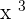 , we have used the power rule which says that if
, we have used the power rule which says that if  , then
, then  .
.
Now, multiply 7 with the term inside the brackets to get the final value of 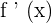 .
.
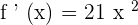
Example 2
Find the derivative of the function  .
.
Solution
You can notice that in the above function, the fraction 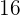 is multiplied by the squared variable
is multiplied by the squared variable 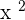 . Hence, we can write the function as a product of fraction and variable like this:
. Hence, we can write the function as a product of fraction and variable like this:
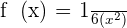
Now, use the derivative power rule 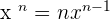 to get the derivative of the function inside parentheses:
to get the derivative of the function inside parentheses:
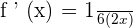
We will get the following final answer after simplifying the above derivative:
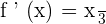
Derivative of x
The derivative of  is 1 because when we will apply the power rule, we will get the exponent 0 of the variable
is 1 because when we will apply the power rule, we will get the exponent 0 of the variable  . Since,
. Since, 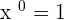 , hence as a general rule we can say that the derivative of
, hence as a general rule we can say that the derivative of  is 1. Mathematically, it can be written as:
is 1. Mathematically, it can be written as:
If  , then
, then 
Derivative Power Rule
We have already used this rule while differentiating the functions in the above examples. The power rule of derivative is expressed as:
If  , then
, then 
Example
Find the derivative of the function  .
.
Solution
We will simply apply the derivative power rule to find the derivative of the above function. Since, in the above function the value of n is 10, hence the derivative of the function will be written as follows using this value of n:
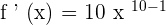
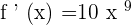
Derivative of a Root
The derivative rule of the root is explained below mathematically:
If  , then
, then 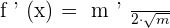
The above formula is for the derivative of a function which involves a square root. If you have to find the derivative of a root function other than square root, then the following formula should be used:
If 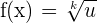 , then
, then 
Let us explain the above rule by the following examples.
Example 1
Find the derivative of the function 
Solution
The derivative of the term inside the root symbol is 6. Using the derivative square root formula 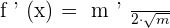 , we will write the final answer as follows:
, we will write the final answer as follows:

To simplify the above answer, we will simply divide the numerator and the denominator by 2:
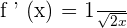
Example 2
Find the derivative of the function 
Solution
To find the derivative of the above function, use the formula  .
.
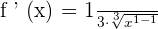
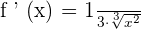
It can also be written as:
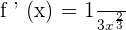
Derivative of a Sum or Difference
The derivative of a sum or difference of two numbers is equal to the derivatives of individual terms. If m and n are two terms, then their derivative will be calculated as follows:
If 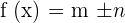 , then
, then 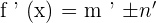
Example 1
Find the derivative of the function 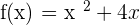 .
.
Solution
To find the derivative of the above function, we will use the derivative sum rule which works by finding the derivative of the individual terms involved in it. The derivative of 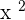 is 2x which is calculated using the power rule and the derivative of 4x is 4. Hence, the derivative of the entire function is given below:
is 2x which is calculated using the power rule and the derivative of 4x is 4. Hence, the derivative of the entire function is given below:
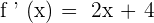
Example 2
Find the derivative of the function  .
.
Solution
Find the derivatives of the individual terms involved in the function. The derivative of 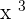 is
is 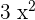 and the derivative of 5x is 5.
and the derivative of 5x is 5.

Derivative Product Rule
The mathematical notation of the derivative product rule is given below:
If  , then
, then 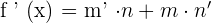
The above rule is explained by the following example.
Example
Find the derivative of the function 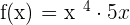 .
.
Solution
Find the derivative of individual factors involved in the above function. The derivative of 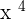 is
is  and the derivative of 5x is 5. Hence, using the formula
and the derivative of 5x is 5. Hence, using the formula  , then
, then 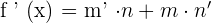 , we will write the derivative of the whole function like this:
, we will write the derivative of the whole function like this:
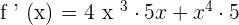

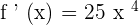
Derivative Quotient Rule
The derivative quotient rule is expressed mathematically as:
If 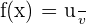 , then
, then 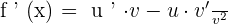
Example
Find the derivative of the function 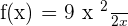 .
.
Solution
The derivative of the term 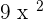 is 18x and the derivative of the term 2x is equal to 2. We will put these values in the quotient derivative formula which says that if
is 18x and the derivative of the term 2x is equal to 2. We will put these values in the quotient derivative formula which says that if 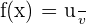 , then
, then 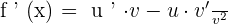 :
:
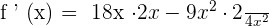


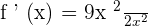

Derivative Reciprocal Rule
The derivative reciprocal rule is mathematically denoted as follows:
If 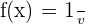 , then
, then 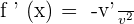
Example
Find the derivative of the function 
Solution
Since, the above function is in the reciprocal form, therefore we will use the derivative formula 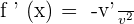 to find the derivative. The derivative of the function
to find the derivative. The derivative of the function 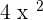 is
is 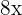 . Put this value in the formula to get the derivative:
. Put this value in the formula to get the derivative:
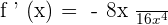
Divide the the terms in the numerator and the denominator by - 8x:

Derivative of an Exponential Function
The derivative of the exponential functions is mathematically denoted as:
If 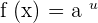 , then
, then 
Example
Find the derivative of the exponential function 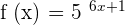 .
.
Solution
We will find the derivative of the above function in four steps:
Step 1 - First write the function as it is 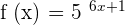
Step 2 - Find the derivative of the function in power. The derivative of the function in the exponent is a linear equation. We know that the the derivative of a linear function is equal to its slope, hence its derivative will be equal 6.
Step 3 - Find the logarithm of the base. The base in the above function is 5, so its log will be written as 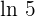 .
.
Step 4 - We will get the derivative of the whole function by multiplying the terms obtained in step 1, 2 and 3:
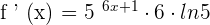
Derivative of a Logarithmic Function
The mathematical notation of the derivative of the logarithmic functions is given below:
If 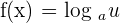 , then
, then 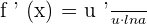
Example
Find the derivative of the logarithmic function 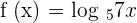 .
.
Solution
First, find the derivative of 7x. The derivative of 7x is 7. Put this value in the formula 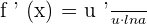 .
.

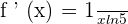
Derivative of a Sine Function
The mathematical notation of this derivative rule is given below:
If  , then
, then 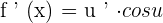
Example
Find the derivative of the function 
Solution
The derivative of  is 6. Put this value in the formula
is 6. Put this value in the formula 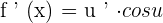 .
.

Derivative of a Cosine Function
The derivative of a cosine function is mathematically denoted as follows:
If  , then
, then 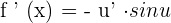
Example
Find the derivative of the function 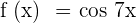
Solution
The derivative of the term  is 7. Putting this value in the formula we will get:
is 7. Putting this value in the formula we will get:
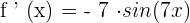
Derivative of a Tangent Function
The derivative of a tangent function is mathematically denoted as follows:
If 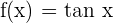 , then
, then 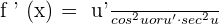
In the above formula, cos represents cosine function and sec represent secant function.
Example
Find the derivative of the tangent function 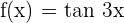 .
.
Solution
The derivative of the term 3x is 3. Put this value in the tangent formula to get the following answer:
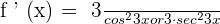
Derivative Chain Rule
We find the derivative chain rule to find the derivative of a composite function. We use the derivative chain rule when we have a function inside another function. Mathematically the derivative chain rule is denoted as follows:
If there is a 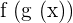 , then its derivative is
, then its derivative is 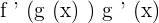
Example
Find the derivative of the function  .
.
Solution
We cannot solve the above function using any of the above differentiation rules except the chain rule because this is a composite function. There is a function inside another function. First, we have a function  and then we are taking the cube of the entire function. We can say that
and then we are taking the cube of the entire function. We can say that  and
and 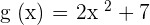 . When we will write the function as
. When we will write the function as 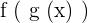 , we will get the function
, we will get the function 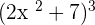 .
.
Using the derivative chain rule, we will write the derivative of the function as follows:
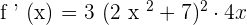
We can rewrite it after simplification as follows:

Summarise with AI:













Like the explanation, want to rearn more. Really enjoying the documents received.