Chapters
Till now you have understood what is calculus? Why do we use calculus? And most importantly, how to find the rate of change of anything (i.e. derivatives). The next lecture is about product and quotient rules. Suppose you are asked to find the derivative of  , you will simply shout
, you will simply shout 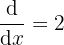 unfortunately, the world of calculus isn't that easy as you think, let's dig down a little bit more. Let's say now you are asked to find the derivatives of
unfortunately, the world of calculus isn't that easy as you think, let's dig down a little bit more. Let's say now you are asked to find the derivatives of 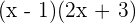 and
and 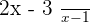 and now, you are confused, you are wondering how to find the derivative of this function? Don't worry, what you need to learn is the product rule and then it will all become a piece of cake.
and now, you are confused, you are wondering how to find the derivative of this function? Don't worry, what you need to learn is the product rule and then it will all become a piece of cake.

Product Rule
Product rule is applied with you have two different functions that are multiplying under a function. For example, you have two functions,  and
and 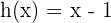 and they both are multiplied under a single function,
and they both are multiplied under a single function,  . Let's denote them with "u" and "v",
. Let's denote them with "u" and "v",  . To find derivative of such functions, you need to use the product rule and here is how you to use product rule:
. To find derivative of such functions, you need to use the product rule and here is how you to use product rule:
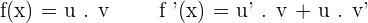
Let's try to understand what is going on here. The answer will consist of two terms, the first function (indicated by "u") is derivated and then multiplied with the second function (indicated by "v"). In the second term, the first function is multiplied with the derivated form of the second function. The key point to note is that one function will be derivated while the other function isn't and both functions are multiplied. If can switch the terms as well, for example, we wrote it like this  , you wrote it like this
, you wrote it like this 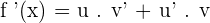 , both will result in the same hence arrangement doesn't matter here.
, both will result in the same hence arrangement doesn't matter here.
Quotient Rule
Quotient rule is applied with both functions are divided with each other. Let's have a look at our previous example, two functions,  and
and 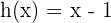 , final function
, final function 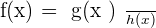 , convert it in the form of "u" and "v",
, convert it in the form of "u" and "v", 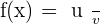 , find derivative of
, find derivative of  . To find the derivative of such functions, you will need the help of quotient rule and here is how you use quotient rule:
. To find the derivative of such functions, you will need the help of quotient rule and here is how you use quotient rule:

Unlike product rule, the quotient rule primarily rely on the arrangement, hence you have to use it exactly the same orelse you will end up with something which isn't correct. To make it more interesting, let's make the  a constant instead of variable. We all know in calculus, our primarily focus is on the variable. Since the constant is in numerator, we will not even touch it, instead our concern will be the denominator (which has a variable). Let's check out how to find derivative of such questions:
a constant instead of variable. We all know in calculus, our primarily focus is on the variable. Since the constant is in numerator, we will not even touch it, instead our concern will be the denominator (which has a variable). Let's check out how to find derivative of such questions:
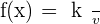 where k is the constant.
where k is the constant.
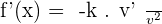
Reciprocal Rule
Forget about the constant now, let's say you are left with a denominator that has a variable and you want to find the derivative of the function. For better clarity, this is your function now,  . That is where the reciprocal rule will save your day. Here is how you use the reciprocal rule:
. That is where the reciprocal rule will save your day. Here is how you use the reciprocal rule:
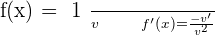
The denominator will be shifted to the numerator and then it will be derivated while the denominator will be squared.
Examples
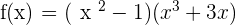
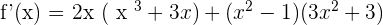

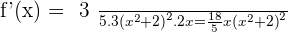

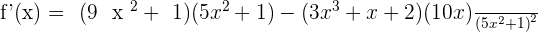
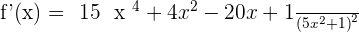
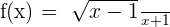
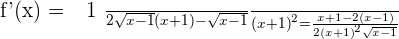
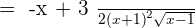


Summarise with AI:












Like the explanation, want to rearn more. Really enjoying the documents received.