Chapters

Limit Formulas
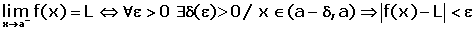
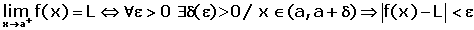
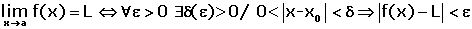

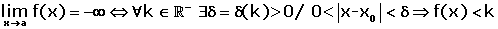
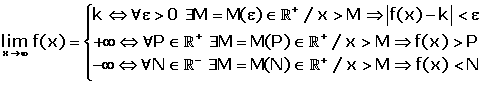

 \lim _ {x \rightarrow a} k = k
\lim _ {x \rightarrow a} k = k 
 \lim _ {x \rightarrow a} [ f (x) \pm g (x) ] = \lim _ { x \rightarrow a} f(x) \pm \lim _ { x \rightarrow a} g(x)
\lim _ {x \rightarrow a} [ f (x) \pm g (x) ] = \lim _ { x \rightarrow a} f(x) \pm \lim _ { x \rightarrow a} g(x) 
 \lim _ {x \rightarrow a} [ f (x) \cdot g (x) ] = \lim _ { x \rightarrow a} f(x) \cdot \lim _ { x \rightarrow a} g(x)
\lim _ {x \rightarrow a} [ f (x) \cdot g (x) ] = \lim _ { x \rightarrow a} f(x) \cdot \lim _ { x \rightarrow a} g(x) 
 \lim _ {x \rightarrow a} \frac { f(x) } { g (x)} = \frac { \lim_ {x \rightarrow a} f(x) } { \lim _{x \rightarrow a} g(x) } if \lim _ {x \rightarrow a} g(x) \neq 0
\lim _ {x \rightarrow a} \frac { f(x) } { g (x)} = \frac { \lim_ {x \rightarrow a} f(x) } { \lim _{x \rightarrow a} g(x) } if \lim _ {x \rightarrow a} g(x) \neq 0 
 \lim_ {x \rightarrow a} [f (x) ^ {g (x)}] = \lim_ {x \rightarrow} [f(x) ] ^ {\lim _ {x \rightarrow a} g(x)} if f(x) >0
\lim_ {x \rightarrow a} [f (x) ^ {g (x)}] = \lim_ {x \rightarrow} [f(x) ] ^ {\lim _ {x \rightarrow a} g(x)} if f(x) >0
 \lim_ {x \rightarrow a} g[f (x)] = g [ \lim _ {x \rightarrow a} f(x) ]
\lim_ {x \rightarrow a} g[f (x)] = g [ \lim _ {x \rightarrow a} f(x) ]
g can be a root, a log, sin, cos, tan, etc.
 \lim_ {x \rightarrow a} \sqrt [n] {f (x)} = \sqrt [n] { \lim_ {x \rightarrow a} f(x)}
\lim_ {x \rightarrow a} \sqrt [n] {f (x)} = \sqrt [n] { \lim_ {x \rightarrow a} f(x)}
 \lim _ {x \rightarrow a} [log _ a f(x)] = log _a [\lim_ {x \rightarrow a} f(x) ] if a >0 and f(x) > 0
\lim _ {x \rightarrow a} [log _ a f(x)] = log _a [\lim_ {x \rightarrow a} f(x) ] if a >0 and f(x) > 0
L' Hospital Rule
 \lim _ { x \rightarrow a} \frac {f(x)} {g (x)} = \lim _ { x \rightarrow a} \frac {f ' (x)} {g ' (x)}
\lim _ { x \rightarrow a} \frac {f(x)} {g (x)} = \lim _ { x \rightarrow a} \frac {f ' (x)} {g ' (x)}
Continuity Formulas
Continuous Function at a Point
 \ni f (a)
\ni f (a)
 \ni \lim _ {x \rightarrow a} f(x) \leftrightarrow \lim _ {x \rightarrow a ^ {-}} f(x) = \lim_ { x \rightarrow a^ {+}} f(x)
\ni \lim _ {x \rightarrow a} f(x) \leftrightarrow \lim _ {x \rightarrow a ^ {-}} f(x) = \lim_ { x \rightarrow a^ {+}} f(x)
 f(a) = \lim {x \rightarrow a} f(x)
f(a) = \lim {x \rightarrow a} f(x)
Directional Continuity
Left-Continuous Function
 f(a) = \lim _ {x \rightarrow a ^ {-}} f(x)
f(a) = \lim _ {x \rightarrow a ^ {-}} f(x)
Right-Continuous Function
 f(a) = \lim _ {x \rightarrow a ^ {+}} f(x)
f(a) = \lim _ {x \rightarrow a ^ {+}} f(x)
Discontinuity
Removable Discontinuity
 ∃ f (a) or f(a) \neq \lim _ {x \rightarrow a} f(x)
∃ f (a) or f(a) \neq \lim _ {x \rightarrow a} f(x)
Jump Discontinuity
 \lim _ {x \rightarrow a ^ {-}} f(x) \neq \lim _ {x \rightarrow a ^ {+}} f(x)
\lim _ {x \rightarrow a ^ {-}} f(x) \neq \lim _ {x \rightarrow a ^ {+}} f(x)
Essential Discontinuity

Derivative Formulas
u and v are functions of x.
a, e and k are constants (real numbers)

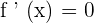
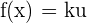
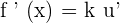


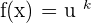
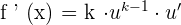

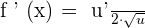
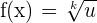


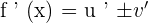
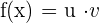
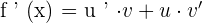
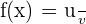





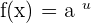
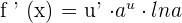
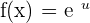
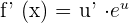
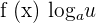

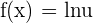


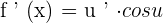

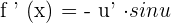
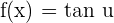
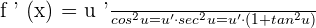
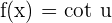
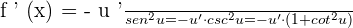
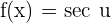
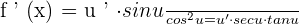
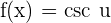
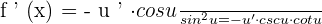
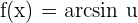
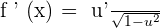

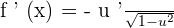
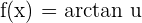
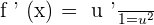
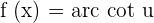


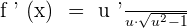
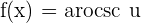


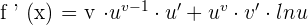
Chain Rule
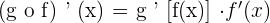
Derivative of an Implicit Function
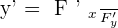
Integrals Formulas
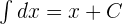
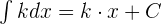
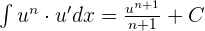
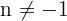



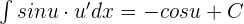
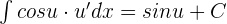
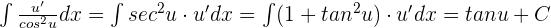

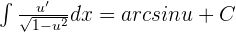
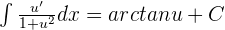
Integration by Parts

Integration by Substitution
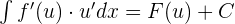
Change of Variables
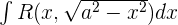

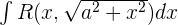
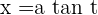

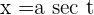

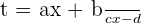
If 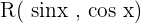 is even
is even
Change 
sin x 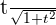
cos x 
tan x t
dx 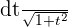
If 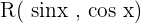 is not even:
is not even:
Change 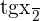
sen x 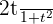
cos x 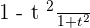
tgx 
dx 
Definite Integral
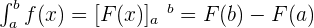

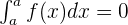

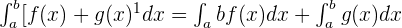
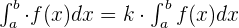
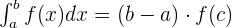

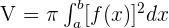
Summarise with AI:













Like the explanation, want to rearn more. Really enjoying the documents received.