Chapters
- What are Trigonometric Functions?
- Derivative of the Sine Function
- Derivative of the Cosine Function
- Derivative of the Tangent Function
- Derivative of the Cotangent Function
- Derivative of the Secant Function
- Derivative of the Cosecant Function
- Examples of Derivatives of Trigonometric Functions
- Example 1
- Example 2
- Example 3
- Example 4
- Example 5
- Example 6
- Example 7
- Example 8
- Example 9
- Example 10
- Example 11
Finding a derivative of a function is an important concept of calculus. The derivative of a function is defined as follows:
"A derivative is an instantaneous rate of change of a function at a given point"
The process of finding derivatives is known as differentiation. The two types of functions that are generally differentiated are explicit and implicit functions. In this article, we will study how to differentiate explicit trigonometric functions. We use differentiation rules to find the derivatives of explicit functions. Some of the common rules of differentiation are constant rule, sum rule, difference rule, power rule, product rule, quotient rule (used for fractions), and chain rule.
Before proceeding to the relevant formulae and examples, let us find out what are the trigonometric functions first.

What are Trigonometric Functions?
Trigonometry is an important branch of mathematics in which we study the relationship between sides and angles of the triangle. Trigonometric functions tell us how the angles of a triangle are related to its sides. The other names for trig functions are circular functions, goniometric, and angle functions. However, the word "trigonometric" is widely used to describe these kinds of functions. The most common trigonometric functions are sine, cosine, tangent, cotangent, co-secant, and secant. The inverse functions of trig functions are known as inverse trigonometric functions. Inverse trig functions are also known as arcus functions, cyclometric functions, or anti trigonometric functions.
Before proceeding to examples let us find out the derivatives of common trigonometric functions. It is always the best idea to memorize them as they are used to differentiate the functions that involve trigonometric functions.
Derivative of the Sine Function
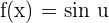
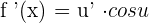
Derivative of the Cosine Function

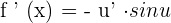
Derivative of the Tangent Function
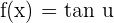
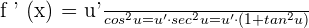
Derivative of the Cotangent Function
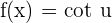
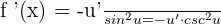
It is also equal to 
Derivative of the Secant Function
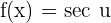

Derivative of the Cosecant Function
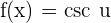

Examples of Derivatives of Trigonometric Functions
Example 1
Compute the derivative of 
Solution
Let 
We know that if 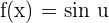 , then
, then 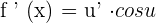 .It means that we will multiply the derivative of the inner function u with the derivative of the outer function sin.
.It means that we will multiply the derivative of the inner function u with the derivative of the outer function sin.
In this example,  . Therefore,
. Therefore, 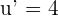 . We will substitute it in the above formula to get the final answer:
. We will substitute it in the above formula to get the final answer:
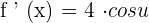
Since  , hence
, hence 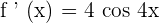 .
.
Example 2
Differentiate 
Solution
Suppose  .
.
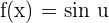
We know that if 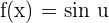 , then
, then 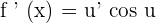 .
.
Here, u = 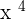 . We will apply power rule to find u '.
. We will apply power rule to find u '.
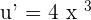
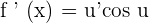
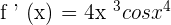
Example 3
Differentiate 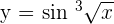
Solution
This is a complex trig function. We will use chain rule again and again to find the derivative of this function.
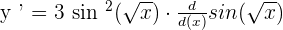
Remember that 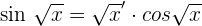 .
.
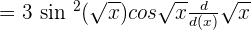
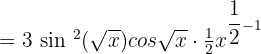
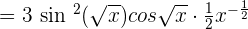

Example 4
Differentiate 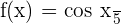
Solution
This function can be written as 
We know that the derivative of a cosine function is  . In the above function,
. In the above function, 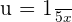 , therefore
, therefore 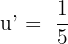
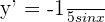
Example 5
Differentiate 
Solution
Suppose 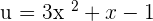 .
.
We know that if  , then
, then 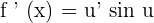 . It means that the derivative of the inner function will be multiplied with the derivative of the outer function cosine.
. It means that the derivative of the inner function will be multiplied with the derivative of the outer function cosine.
If 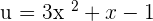 , then
, then 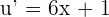 .
.
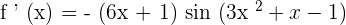
Example 6
Differentiate 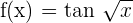
Solution
Suppose 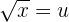 .
.
We know that if 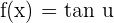 , then
, then 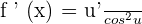
Here, 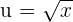 . Hence,
. Hence,  .
.

Example 7
Differentiate 
Solution
Suppose 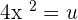 .
.
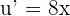
We know that if 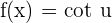 , then
, then 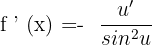 .
.

Example 8
Differentiate 
Solution
Suppose 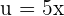
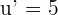
We know that if 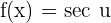 , then
, then  . Now, we will substitute
. Now, we will substitute 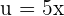 and
and 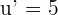 to get the derivative of the function.
to get the derivative of the function.

Example 9
Differentiate 
Solution
Suppose 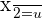 .
.
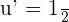
We know that if 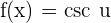 , then
, then 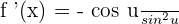
The substitution of 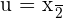 and
and 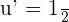 will get us the final answer of this question.
will get us the final answer of this question.
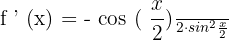
Example 10
Differentiate 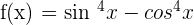 .
.
Solution
This function involves two trigonometric functions, sine, and cosine. To differentiate this function, we will use the derivative difference rule and derivative power rule.
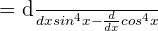
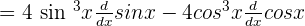
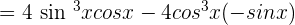
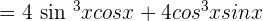
We will simplify and rewrite it as:
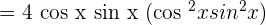
Example 11
Differentiate 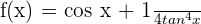
Solution
We will use the derivative sum rule to differentiate the above function.
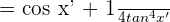
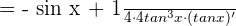
After simplification, we will get the following derivative of the function.
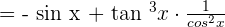
Summarise with AI:













Like the explanation, want to rearn more. Really enjoying the documents received.