Chapters
- What are Derivatives?
- What are Trigonometric Functions?
- What are Inverse Trigonometric Functions?
- Finding Derivatives of Inverse Trigonometric Functions
- Derivative of the Arcsine Function
- Derivative of the Arccosine Function
- Derivative of the Arctangent Function
- Derivative of the Arccotangent Function
- Derivative of the Arcsecant Function
- Derivative of the Arccosecant Function
- Examples of Derivatives of Inverse Trigonometric Functions
In this article, we will learn how to compute the derivatives of the inverse trigonometric functions. Before discussing the formulas and procedure of finding the derivatives of inverse trigonometric functions, first, let us see what are derivatives, trigonometric functions, and their inverses.

What are Derivatives?
Derivatives of the functions represent instantaneous rates of change of the functions at given points. The process of finding the derivatives of functions is called differentiation and its inverse is known as integration. Finding derivatives is an essential part of differential calculus. We solve many complex problems in calculus by differentiating the functions. We have several rules of differentiation which help us to find derivatives easily. The most commonly used rules are derivative sum or differentiation rule, product rule, quotient rule, chain rule, and power rule.
What are Trigonometric Functions?
We describe trigonometric functions as elementary functions. The foundation of the arguments of trigonometric functions is angles because they tell us the relationship between the angles and sides of a right-angled triangle. You may come across these functions while solving differential equations. There are six trigonometric functions known as sine, cosine, tangent, cotangent, secant, and cosecant.
What are Inverse Trigonometric Functions?
The inverse trigonometric functions are inverses of the trigonometric functions. The inverse trigonometric functions have other names too that are used occasionally. For instance, they are also known as anti-trigonometric functions or cyclometric functions. Like trigonometric functions, the applications of inverse trigonometric functions are also widespread in the fields of geometry, engineering, and physics. Every trigonometric function has its inverse, that is why there are six inverse trigonometric functions.
- The inverse of a sine function is the arcsine
- The inverse of a cosine function is the arccosine
- The inverse of a tangent function is the arctangent
- The inverse of a cotangent function is the arc cotangent
- The inverse of a secant function is the arcsecant
- The inverse of a cosecant function is the arccosecant
Finding Derivatives of Inverse Trigonometric Functions
In this section, we will discuss the formulas to compute the derivatives of inverse trigonometric functions.
Derivative of the Arcsine Function
f(x) = arcsin u 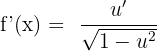
Derivative of the Arccosine Function
f(x) = arccos u 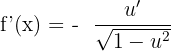
Derivative of the Arctangent Function
f(x) = arctan u 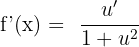
Derivative of the Arccotangent Function
f(x) = arc cot u 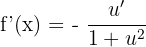
Derivative of the Arcsecant Function
f(x) = arc sec u 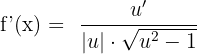
Derivative of the Arccosecant Function
f(x) = arccsc u 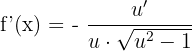
Examples of Derivatives of Inverse Trigonometric Functions
In this section, we will solve some examples in which we will use the formulas of the inverse trigonometric functions to compute the derivatives.
Example 1
Differentiate 
Solution
First, we will identify u. Here,  . The derivative of u is u' = 2x. Substitute these values of u and u' in the below formula to get the derivative of this arcsine function:
. The derivative of u is u' = 2x. Substitute these values of u and u' in the below formula to get the derivative of this arcsine function:
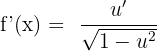
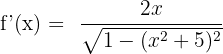
We will simplify the expression by taking a square of  .
.
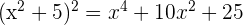
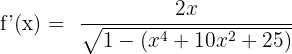
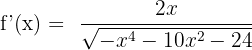
Example 2
Find the derivative of the function 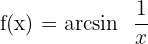 .
.
Solution
First, we will identify u. Here, 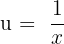 . The derivative of u will be found by using the exponent rule like this:
. The derivative of u will be found by using the exponent rule like this:
 can be written as
can be written as 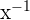 . The derivative of
. The derivative of 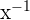 can be found using the exponent rule.
can be found using the exponent rule.

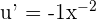
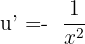
Substitute these values of u and u' in the below formula to get the derivative of this arcsine function:
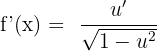
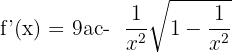
We will write the answer in simplified form like this:
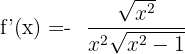
Example 3
Differentiate the function 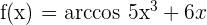
Solution
First, we will identify u. Here, 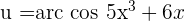 . The derivative of u will be found by using the power and variable multiplied by a constant rule like this:
. The derivative of u will be found by using the power and variable multiplied by a constant rule like this:

Substitute these values of u and u' in the below formula to get the derivative of this arcsine function:
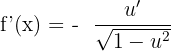
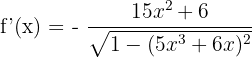
Now, we will compute the square of  to simplify the above answer.
to simplify the above answer.
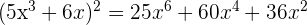
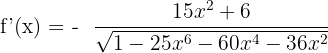
Example 4
Differentiate the function 
Solution
First, we will identify u in the above function. Here,  . In the next step, we will be differentiating u. Since, u has a positive sign between the elements, hence we will use sum/differentiation rule to differentiate it.
. In the next step, we will be differentiating u. Since, u has a positive sign between the elements, hence we will use sum/differentiation rule to differentiate it.
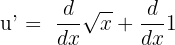
 can be written as
can be written as 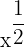 . We can differentiate it using the exponent rule like this:
. We can differentiate it using the exponent rule like this:
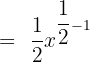
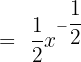
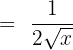
The derivative of 1 is 0 because it is a constant, hence, 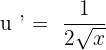 .
.
Substitute these values of u and u' in the formula below:
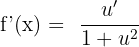
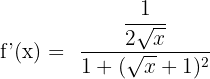
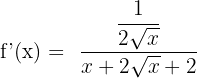
Example 5
Differentiate the function 
Solution
First, we need to identify u in the above function. Here, u = 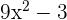 . The derivative of u can be found easily using the derivative sum/difference and power rule. The derivative of
. The derivative of u can be found easily using the derivative sum/difference and power rule. The derivative of  is equal to 18x and the derivative of the constant 3 is equal to 0. Hence, the value of u' = 18x.
is equal to 18x and the derivative of the constant 3 is equal to 0. Hence, the value of u' = 18x.
Substitute these values of u and u' in the formula of finding the derivative of arc cotangent function:
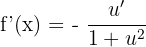
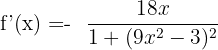
To simplify the above expression, we need to take the square of the function 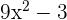 .
.

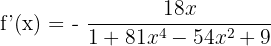
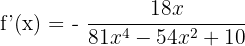
Example 6
Find the derivative of the function  .
.
Solution
First, we will identify u in the above function. Here,  . Next, we need to find the derivative of
. Next, we need to find the derivative of  using the sum/difference and exponent rules. The derivative of
using the sum/difference and exponent rules. The derivative of  is equal to 2x and the derivative of 2x is equal to 2.
is equal to 2x and the derivative of 2x is equal to 2.
Hence, u' = 2x + 2
Substitute these values of u and u' in the below formula of finding the derivative of an arccosecant function:
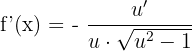
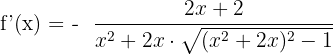
We will simplify the above expression by taking a square of 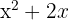 .
.
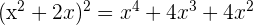
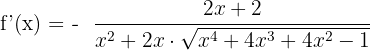
Summarise with AI:













Like the explanation, want to rearn more. Really enjoying the documents received.