Chapters
In this article, you will learn what is a tangent line and how to find an equation of the tangent line. You will often come across problems in Calculus where you are asked to find an equation of the line tangent to a curve. We find this equation of the tangent line using the first derivative. While solving the problems related to the equations of the tangent line, you should keep the following things in mind:
- A line that touches the curve at a single point only is known as a tangent line.
- The slope-intercept form of the equation of a line is y = mx + b. Here, m represents the slope of a line and b depicts the y-intercept.
- The equation of the line in point-slope form is
 . This form of the equation employs a point on the line which is reflected by
. This form of the equation employs a point on the line which is reflected by  . The slope of the line is represented by m.
. The slope of the line is represented by m. - Slope means the average rate of change of the function at a given point. For calculating the slope, we need to plug in the values of
 and
and  in the following slope formula:
in the following slope formula:
Slope = 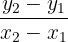

Slope of the Tangent Line

The slope of the tangent to a curve at a point is the derivative of the function at that point as shown in the above graph.
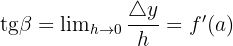
The line tangent to a curve at a point is one that passes through the point (a, f(a)) and whose slope is equal to f '(a).
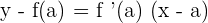
What is a Derivative?
Regarding the derivative of a function, you must know that the derivative represents an instantaneous rate of change of a function at a given point. Geometrically, the first derivative represents the slope of the line. In other words, we can say that the slope of the line tangent to a curve represents the first derivative.
We denote the derivative of a function in the following ways:
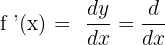
The formula for computing the derivative of a function using limit is given below:
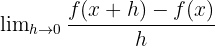
We can even find the higher order derivatives of a function, i.e. derivative of a derivative. These derivatives are known as second derivative, third derivative, and fourth derivative respectively. We can find the derivatives using certain rules of differentiation such as sum/difference rule, product rule, power rule, quotient rule, and chain rule etc.
Steps to Find Equation of a Tangent Line to a Curve
Here are some of the steps to find an equation of a tangent line to a curve:
- Find the first derivative of the function
- Substitute the value of a point in the derivative to get the slope of the line
- Find y-coordinate of the equation by substituting the point at which the line touches the curve in the original equation.
- Now, you have both x-y coordinates, hence you can easily substitute these values in the point-slope form of the equation and convert it into the slope-intercept form.
In the next section, we will solve some examples in which we will find the equation of the tangent line.
Example 1
Find the equation of the line tangent to 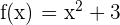 at
at 
Solution
First, we need to find the derivative of the function using the sum/difference and power rules. The derivative of  is equal to 2x and the derivative of 3 is zero.
is equal to 2x and the derivative of 3 is zero.

Now, the next step is to calculate the slope of the tangent line through the derivative of the function. It is given in the example that the line is tangent at x = 3. Hence, we will substitute 3 in the above derivative to get the slope of the tangent line:
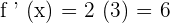
Hence, the slope of the tangent line is 6.
To be able to come up with an equation of a tangent line, we must know points of the line. It is given that line is tangent at x =3. Hence, we have x-coordinate of the line. To find the y-coordinate, we will substitute  in the equation
in the equation 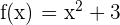
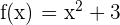
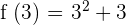
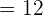
Hence, we have got the points 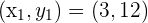 . Hence, we can easily formulate the equation of the line using the following point slope form:
. Hence, we can easily formulate the equation of the line using the following point slope form:

Substitute 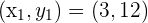 in the above equation:
in the above equation:
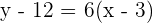
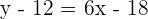
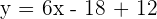
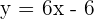
Hence, the equation of the line is 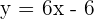 , where 6 is the slope and -6 is the y-intercept of the line.
, where 6 is the slope and -6 is the y-intercept of the line.
Example 2
Find the equation of the line tangent to the parabola 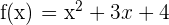 at
at 
Solution
First, we need to find the derivative of the quadratic function in this example which is given in standard form using the sum/difference and power rules. The derivative of  is equal to 2x, the derivative of 3x is 3, and the derivative of the constant 4 is equal to zero.
is equal to 2x, the derivative of 3x is 3, and the derivative of the constant 4 is equal to zero.
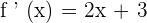
Now, the next step is to calculate the slope of the tangent line through the derivative of the function. It is given in the example that the line is tangent at x = -1. Hence, we will substitute -1 in the above derivative to get the slope of the tangent line:

Hence, the slope of the tangent line is 1.
To be able to come up with an equation of a tangent line, we must know points of the line. It is given that line is tangent at x =-1. Hence, we have x-coordinate of the line. To find the y-coordinate, we will substitute  in the equation
in the equation 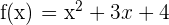
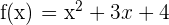

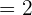
Hence, we have got the points 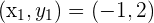 . Hence, we can easily formulate the equation of the line using the following point slope form:
. Hence, we can easily formulate the equation of the line using the following point slope form:

Substitute 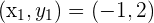 in the above equation:
in the above equation:



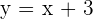
Hence, the equation of the line is 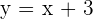 , where 1 is the slope and 3 is the y-intercept of the line.
, where 1 is the slope and 3 is the y-intercept of the line.
Example 3
Find the equation of the line tangent to 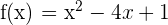 at
at 
Solution
First, we need to find the derivative of the function using the sum/difference and power rules. The derivative of  is equal to 2x. the derivative of -4x is equal to -4 and the derivative of the constant 1 is equal to 0.
is equal to 2x. the derivative of -4x is equal to -4 and the derivative of the constant 1 is equal to 0.

Now, the next step is to calculate the slope of the tangent line through the derivative of the function. It is given in the example that the line is tangent at x = 4. Hence, we will substitute 4 in the above derivative to get the slope of the tangent line:

Hence, the slope of the tangent line is 4.
To be able to come up with an equation of a tangent line, we must know points of the line. It is given that line is tangent at x = 4. Hence, we have x-coordinate of the line. To find the y-coordinate, we will substitute  in the equation
in the equation 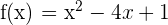
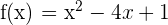
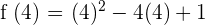
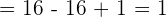
Hence, we have got the points 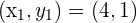 . Hence, we can easily formulate the equation of the line using the following point slope form:
. Hence, we can easily formulate the equation of the line using the following point slope form:

Substitute 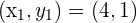 in the above equation:
in the above equation:
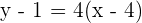
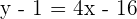
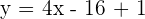
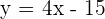
Hence, the equation of the line is 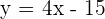 , where 4 is the slope and -15 is the y-intercept of the line.
, where 4 is the slope and -15 is the y-intercept of the line.
Summarise with AI:












Like the explanation, want to rearn more. Really enjoying the documents received.