
When a Function is Differentiable and Continuous?
In this article, you will learn what is meant by the differentiability and continuity of a function. First, let us see when a function is continuous and differentiable at a point:
If a function is differentiable at point x = a, then the function is continuous at x = a.
The reciprocal may not be true, that is to say, there are functions that are continuous at a point which, however, may not be differentiable.
To understand the differentiability of a function, you must be aware of what is a derivative. A derivative of a function depicts an instantaneous rate of change of a function at a given point. The process of finding the derivative of a function is known as differentiation and the inverse of differentiation is called integration.
We can differentiate a function until a point it is no longer differentiable, i.e., we can compute the derivative of a function, and then we can also take the derivative of the derivative. The derivative of the function  is denoted by
is denoted by 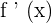 and the derivative of
and the derivative of 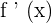 is
is 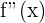 . The derivative of a function is known as the first derivative and as we go further to take more derivatives, we name those as second, third, fourth and so on derivatives. The three notations for derivatives are given below:
. The derivative of a function is known as the first derivative and as we go further to take more derivatives, we name those as second, third, fourth and so on derivatives. The three notations for derivatives are given below:
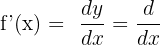
Usually, we find the derivative of a function using the rules of derivatives. These rules are known as sum/difference rule, power rule, quotient rule, chain rule, and product rule, etc.
To explain the differentiability and continuity of a derivative of a function that is differentiable and continuous at point a we use the following formula of the derivative:
 f ' (a) = \lim_{x \rightarrow a} \frac{f(x) - f(a)}{x - a}
f ' (a) = \lim_{x \rightarrow a} \frac{f(x) - f(a)}{x - a}
In the next section, we will study the continuity and differentiability of some functions.
Example 1
State that whether the following function is differentiable and continuous at x = 0:
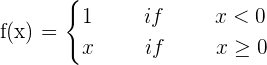
Solution
To state whether the above function is differentiable and continuous, we will study the continuity of the function first. This is because if a function is not continuous then it is also not differentiable. To study the continuity of the function, we need to substitute x = 0 in both the functions:
 f(x) = \lim_ {x \rightarrow 0^{-}}1 = 1
f(x) = \lim_ {x \rightarrow 0^{-}}1 = 1
Now, we will substitute x = 0 in the second function like this:
 f(x) = \lim_{x \rightarrow 0^{+}} x = 0
f(x) = \lim_{x \rightarrow 0^{+}} x = 0
After substituting  in both the functions, we get different results. Substituting 0 in the first function yields 1 and the substitution in the second functions gives us 0. So, we can say that the function is not continuous. Since the function is not continuous at
in both the functions, we get different results. Substituting 0 in the first function yields 1 and the substitution in the second functions gives us 0. So, we can say that the function is not continuous. Since the function is not continuous at  , so it is also not differentiable.
, so it is also not differentiable.
Example 2
State that whether the following function is differentiable and continuous at x = 4:
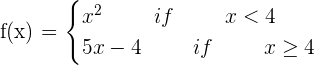
Solution
To state whether the above function is differentiable and continuous, we will study the continuity of the function first. This is because if a function is not continuous then it is also not differentiable. To study the continuity of the function, we need to substitute x = 4 in both the functions:
 f(4) = \lim_{x \rightarrow 4^{-}} 4^2 = 16
f(4) = \lim_{x \rightarrow 4^{-}} 4^2 = 16
Now, we will substitute x =4 in the second function:
 f(4) = \lim_{x \rightarrow 4^{+}} 5(4) - 4 = 16
f(4) = \lim_{x \rightarrow 4^{+}} 5(4) - 4 = 16
After substituting 4 in both the functions, we get the answer 16. Hence, the function is continuous at x = 4. Now, we will see if the function is differentiable or not. To test the differentiability of the function, we need to use the following formula:
 f ' (a) = \lim_{x \rightarrow a} \frac{f(x) - f(a)}{x - a}
f ' (a) = \lim_{x \rightarrow a} \frac{f(x) - f(a)}{x - a}
Put 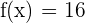 ,
, 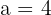 , and
, and  in the above formula:
in the above formula:
 f ' (4^{-}) = \lim_{x \rightarrow 4 ^ {-}} \frac{x^2 - 16}{x - 4}
f ' (4^{-}) = \lim_{x \rightarrow 4 ^ {-}} \frac{x^2 - 16}{x - 4}
 f ' (4^{-}) = \lim_{x \rightarrow 4 ^{-}} \frac{(x - 4) (x + 4)}{x - 4}
f ' (4^{-}) = \lim_{x \rightarrow 4 ^{-}} \frac{(x - 4) (x + 4)}{x - 4}
 f ' (4^{-}) = x + 4
f ' (4^{-}) = x + 4
 f ' (4^{-}) = 4 + 4 = 8
f ' (4^{-}) = 4 + 4 = 8
Now, we will find the derivative of the second part of the function using this formula:
 f ' (a) = \lim_{x \rightarrow a} \frac{f(x) - f(a)}{x - a}
f ' (a) = \lim_{x \rightarrow a} \frac{f(x) - f(a)}{x - a}
 f ' (a) = \lim_{x \rightarrow 4 ^{+}} \frac{5x - 4 - 16}{x - 4}
f ' (a) = \lim_{x \rightarrow 4 ^{+}} \frac{5x - 4 - 16}{x - 4}
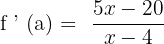
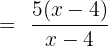
 = 5
= 5
Hence, the function is continuous as well as differentiable at  .
.
Example 3
State that whether the following function is differentiable and continuous at x = 2:
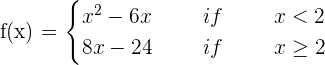
Solution
To state whether the above function is differentiable and continuous, we will study the continuity of the function first. This is because if a function is not continuous then it is also not differentiable. To study the continuity of the function, we need to substitute x = 2 in both the functions. First, we will substitute in the first part of the function.
 f(2) = \lim_{x \rightarrow 2^{-}} 2^2 - 6 (2) = 4 - 12 = -8
f(2) = \lim_{x \rightarrow 2^{-}} 2^2 - 6 (2) = 4 - 12 = -8
Now, we will substitute  in the second part of the function:
in the second part of the function:
 f(2) = \lim_{x \rightarrow 2^{+}} 8(2) - 24 = 16 - 24 = -8
f(2) = \lim_{x \rightarrow 2^{+}} 8(2) - 24 = 16 - 24 = -8
Since after substituting 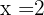 in both the functions, we get the same output, i.e. -8, therefore, it means that the function is continuous at
in both the functions, we get the same output, i.e. -8, therefore, it means that the function is continuous at 
Now, we will see if the function is differentiable or not. To do so, we will substitute the values of  ,
,  and
and  in the following formula:
in the following formula:
 f ' (a) = \lim_{x \rightarrow a} \frac{f(x) - f(a)}{x - a}
f ' (a) = \lim_{x \rightarrow a} \frac{f(x) - f(a)}{x - a}
Substitute  ,
,  and
and  in the above function:
in the above function:
 f ' (a) = \lim_{x \rightarrow a} \frac{x^2 - 6x - (-8)}{(x -2)}
f ' (a) = \lim_{x \rightarrow a} \frac{x^2 - 6x - (-8)}{(x -2)}
 f ' (a) = \lim_{x \rightarrow a} \frac{x^2 - 6x + 8}{(x - 2)}
f ' (a) = \lim_{x \rightarrow a} \frac{x^2 - 6x + 8}{(x - 2)}
 f ' (a) = \lim_{x \rightarrow a} \frac{x^2 - 4x - 2x + 8}{(x - 2)}
f ' (a) = \lim_{x \rightarrow a} \frac{x^2 - 4x - 2x + 8}{(x - 2)}
 f ' (a) = \lim_{x \rightarrow a} \frac{x(x - 4) - 2 (x - 4}{(x - 2)}
f ' (a) = \lim_{x \rightarrow a} \frac{x(x - 4) - 2 (x - 4}{(x - 2)}
 f ' (a) = \lim_{x \rightarrow a} \frac{(x - 4) (x - 2}{(x - 2)}
f ' (a) = \lim_{x \rightarrow a} \frac{(x - 4) (x - 2}{(x - 2)}
 f ' (a) = \lim_{x \rightarrow a} x - 4
f ' (a) = \lim_{x \rightarrow a} x - 4
 f ' (a) = 2 - 4 = -2
f ' (a) = 2 - 4 = -2
Now, we will differentiate the second part of the function by substituting 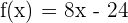 ,
,  and a = 2 in the formula below:
and a = 2 in the formula below:
 f ' (a) = \lim_{x \rightarrow a} \frac{f(x) - f(a)}{x - a}
f ' (a) = \lim_{x \rightarrow a} \frac{f(x) - f(a)}{x - a}
 f ' (a) = \lim_{x \rightarrow 2^{+}} \frac{8x - 24 + 8}{x - 2}
f ' (a) = \lim_{x \rightarrow 2^{+}} \frac{8x - 24 + 8}{x - 2}
 f ' (a) = \lim_{x \rightarrow 2^{+}} \frac{8x - 16}{x - 2}
f ' (a) = \lim_{x \rightarrow 2^{+}} \frac{8x - 16}{x - 2}
 f ' (a) = \lim_{x \rightarrow 2^{+}} \frac{8(x - 2)}{x - 2}
f ' (a) = \lim_{x \rightarrow 2^{+}} \frac{8(x - 2)}{x - 2}
 f ' (a) = 8
f ' (a) = 8
Hence, the function is continuous and differentiable at x = 2.
Example 4
State that whether the following function is differentiable and continuous at x = 1:
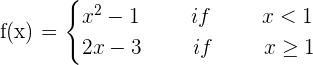
Solution
To state whether the above function is differentiable and continuous, we will study the continuity of the function first. This is because if a function is not continuous then it is also not differentiable. To study the continuity of the function, we need to substitute x = 1 in both the functions:
 f(x) = \lim_ {x \rightarrow 1^{-}}(1)^2 -1 = 0
f(x) = \lim_ {x \rightarrow 1^{-}}(1)^2 -1 = 0
Now, we will substitute x = 1 in the second function like this:
 f(x) = \lim_{x \rightarrow 0^{+}} 2x - 3 = -1
f(x) = \lim_{x \rightarrow 0^{+}} 2x - 3 = -1
After substituting  in both the functions, we get different results. Substituting 1 in the first part of the function yields 0 and 1 in the second part of the function gives -1 as an output. This shows that the function is not continuous. Hence, we can say that the function is neither continuous nor differentiable at x = 1.
in both the functions, we get different results. Substituting 1 in the first part of the function yields 0 and 1 in the second part of the function gives -1 as an output. This shows that the function is not continuous. Hence, we can say that the function is neither continuous nor differentiable at x = 1.












Like the explanation, want to rearn more. Really enjoying the documents received.